Range of Probabilities
You may have heard people say, "That's impossible," or "I'll probably go to the shops tomorrow." These are words that describe the probability or chance of an event happening.
The probability of an event occurring ranges from $0$0 (impossible; it definitely won't happen) to $1$1 (certain; it definitely will happen). We can use fractions or decimals to describe probabilities in between, or even percentages. The picture below shows how:
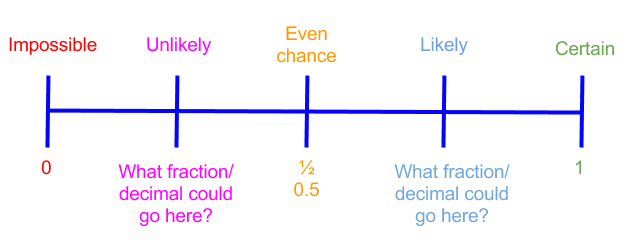
The probability of an event can lie anywhere in between $0$0 and $1$1. For example, a probability of $0.8$0.8 is between $0.5$0.5 and $1$1. Looking at our picture, this means our event is likely to happen.
Words to describe chance
- Certain means an event will always happen, no matter what, e.g. the Sun will rise tomorrow.
- Likely means an event will probably happen but may not, e.g. you will go to school on a Monday (you may be sick or it may be a public holiday)
- Even chance means it's as likely to happen as it is not to happen, e.g. picking a black card out of a deck (there are the same number of red and black cards in a deck).
- Unlikely means an event probably won't happen, e.g. scoring a goal from the halfway line.
- Impossible means an event DEFINITELY won't happen, e.g. your goldfish will grow legs and start walking tomorrow.
Discuss as a class where you think these events will fit in the range of probabilities. Describe using a word, a fraction and a decimal. Then you can think of your own events and do the same!
- Christmas will be on the 25th of December next year.
- It will rain next week.
- Blue is the most popular colour of students in your school.
- You flip a coin and it lands on heads.
Examples
Question 1
A probability of $0.2$0.2 means:
it is impossible for the event to occur
Aan event is likely to occur.
Ban event is unlikely to occur.
Can event is certain to occur.
D
Question 2
Which of these events has a probability closest to $0.9$0.9?
You will flip tails in a coin toss.
AIt will rain somewhere in Australia tomorrow.
BYou will score $110%$110% on the next maths test.
CYou’ll fly a rocket to school.
D