
Shapes in Fractal Geometry
One of the things you might notice about the maths that you study at school is that it is all really old. Most of the geometry you study dates back to Ancient history, the algebra from the Medieval period and even "modern" topics like calculus and probability come from the 17th century. In contrast to subjects like science, where you hear all about new cutting edge discoveries, mathematics seems to be stuck in the past.
However, this could not be further from the truth. Just like science, modern mathematics is full of groundbreaking new discoveries, with game theory, incompleteness theory and chaos theory being just a few examples. In this exercise we're going to introduce you to another important example of modern mathematics, the study of Fractals.
What Is A Fractal?
You may have seen cool-looking patterns like this one before:

Source: User Kh267 / Wikimedia Commons / CC-BY-SA-3.0
These patterns are called fractals. However, not every cool looking pattern is a fractal. Fractals have a very specific definition, which is that they are "self-similiar". This means that they are infinitely detailed, and when you zoom in on any area of a fractal, you will eventually end up looking at a similiar pattern again. For example, in the fractal above can see a big swirl with lots of little swirls coming out of it, and if you look closely at the little swirls, you will see that even tinier swirls are coming off them. This pattern repeats infinitely, with every swirl producing tinier and tinier swirls forever.
The best way to understand this "self-similiarity" is to have a look at a zoomable fractal yourself. Click here to have a look at a zoom-in of the Mandelbrot set, one of the most famous fractals. Notice that as you zoom in, you see the same kinds of patterns over and over again. Here, we'll have a look at some simpler example of fractals, and see how they work.
Koch Snowflake
The Koch Snowflake is one of the most simple fractal patterns. You start with a triangle, then make a set of smaller triangles stick out from each of the sides. After doing this a few times, you get a snowflake pattern, like this:
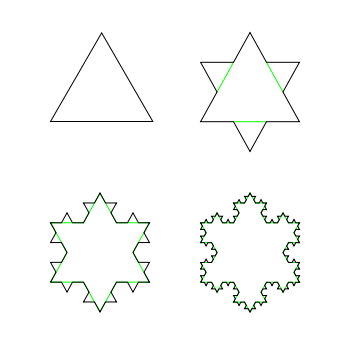
Source: User Wxs / Wikimedia Commons / CC-BY-SA-3.0
Sierpinski Triangle
The Sierpinski triangle is another simple example of a fractal. You take a triangle, break this triangle up into four smaller triangles, and then remove the middle one. You repeat this with the three smaller triangles you have created, and continue doing so infinitely. If you imagine zooming in on the result, you can see that each of the smaller triangles would end up looking just like the bigger triangles, fulfilling the definition of "self-similiarity".

Source: User Wereon / Wikimedia Commons / Public Domain
Sierpinski Carpet
A variation on the same theme is the Sierpinski Carpet. This time, you start with a square, and then break it into 9 pieces and fill the middle one in. You do the same with each of the subsquares, and after a few times you end up with a pattern like this:

Source: User Saperaud~commonswiki / Wikimedia Commons / CC-BY-SA-3.0
Make Your Own Fractal
1. Can you come up with your own fractal pattern? The only definition it has to fulfill is when you zoom in on it, you end up seeing the same pattern again.
Fractals Are Not Limited To Two Dimensions
Most early fractal images focus on two dimensional examples, because these are the easiest to draw and look at. However, the principles of making fractals work just as well in 3D.
Fractals In The Real World
Next time you're in the supermarket, you might notice one of these in the vegetable section:

Source: Jon Sullivan / Wikimedia Commons / Public Domain
This is a Romanesco broccoli, which naturally grows in the shape of a 3D fractal. There are a huge number of other examples of natural processes which also approximate the behaviour of a fractal, including river networks and earthquake fault lines. Fractals appear frequently in nature because, as seen in the previous exercises, they allow complex patterns to be created by very simple rules.
1. What other examples can you think of where fractals might appear in nature?
Fractals in Applied Mathematics
Fractals allow simple rules to lead to complex patterns, which is useful in a wide variety of areas, with computer graphics being one example. When a computer designer wants to create a virtual object, it takes a long time to manually create all of the visual detail of the object. However, using fractals, a set of simple rules can be used to create a very complex object automatically. For example, Space Engine is a game which uses fractals to simulate the entire universe, by using simple rules automatically generate galaxies with billions of stars, and planets with extremely detailed scenery, like the one below:

Source: User Solaris, Space Engine Photo Gallery
The programmer who made this game doesn't even know this world exists. It was made entirely from scratch on the computer of the person playing the game, according to randomly generated fractal patterns.
1. What would be the benefits and disadvantages of generating detail using fractals, as opposed to manually programming them?
Fractals in Pure Mathematics
Just as fractals allow simple rules to make complex patterns, they allow complex patterns to be broken down into simple rules.
For example, let's say a pure mathematician is interested in the distribution of odd numbers in Pascal's Triangle.
1. Make an 8 row Pascal's triangle, and colour in the odd numbers. Recognise the pattern? If it's not clear yet, a bigger Pascal's triangle like this one might help.
2. If the mathematician wanted to know how many odd numbers were in 1000 rows of Pascal's triangle, would they have to write them all out?
3. It has been proven that after continuing the Sierpenski triangle pattern an infinite number of times, the shaded area would approach zero. What does this tell you about the percentage of odd numbers in an infinitely large Pascal's triangle?
The Future Of Fractals
As a fairly new field in mathematics, fractals are still an area of active mathematical research. Mathematicians are still grappling with questions about what fractals are and what can be done with them. During the 21st century, we can expect many advances to be made, opening up new areas of study and leading to new uses of fractals in both pure and applied mathematics.