Deductive reasoning is the process by which a person makes conclusions based on previously known facts. So the aim of a deductive proof is to use other geometric facts to show that a particular equivalence or property exists. This makes writing proofs slightly different to solving geometric properties.

Lets have a look at an example first.

Examples

Question 1

Prove that $x$x & $y$y are supplementary angles.

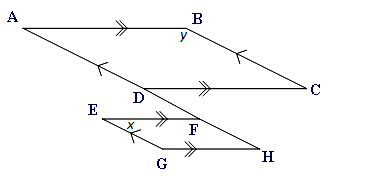
When starting a proof you first need to fully understand what you are being asked to show. In this case we need to know what supplementary means. Supplementary means that the two angles add up to 180°.

To be able to show that two angles add up to 180° we know a few rules that might be useful.

Cointerior angles are supplementary. (U or C rule)

Adjacent angles on a straight line are supplementary.

So if we can show that $x$x and $y$y in the diagram above appear in either of these situations we have shown that $x+y=180$x+y=180°.

Lets see the proof in action.

$\angle EFD=x$∠EFD=x

(Alternate angles on parallel lines are equal)

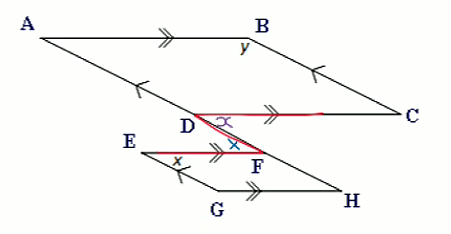
$\angle FDC=x$∠FDC=x

(Alternate angles on parallel lines are equal)

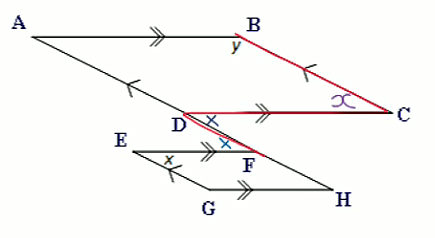
$\angle DCB=x$∠DCB=x

(Alternate angles on parallel lines are equal)

$\angle ABC+\angle BCD=180$∠ABC+∠BCD=180

(Cointerior angles on parallel lines are supplementary)

$y+x=180$y+x=180

$y$y and $x$x are supplementary angles

Question 2

Show that x+y=z

Have a go at solving this one first. What geometric relationships do you see? There is nearly always more than one way to approach these problems, some methods are easier than others. You can see how I solved this one, by watching this video. (see if you can find an even shorter way than I did!)

Here are some sample proofs.

Examples

Question 3

In the following figure, prove that $x$x and $y$y are supplementary.

Question 4

In the diagram, $AC$AC is parallel to $GI$GI. $DF$DF is drawn such that $DF$DF is parallel to $AC$AC and $GI$GI. Prove that $x+y=z$x+y=z

Deductive Proofs