Make the statement true (add/sub)
How can I make this true?
When we looked at whole numbers, we saw that in order to make a statement true, we need to make sure both sides of our number sentence are equal. We can think of it as a set of scales that is evenly balanced.
Now with decimals
We can use the same process for decimal numbers. So, if each block on the scales below represents one tenth, or $0.1$0.1, we can say the scales are balanced since there are $5$5 tenths on each side or $0.5$0.5
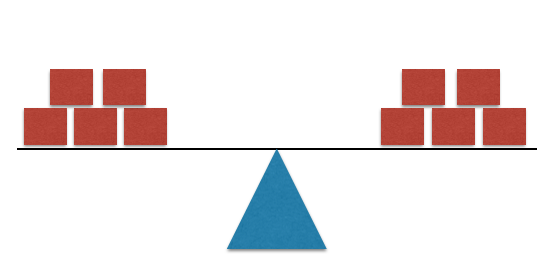
In the first video, we look at decimals with tenths, to see how we make both sides of our number sentence equal. So, for a question like this
we can work out what the ![]() needs to be so that both sides of our equation are equal. We do this by looking at what we are doing to one side and changing the other side. We need to look at both numbers though! We can't just add $4.2$4.2 to the right hand side in our equation above, since the left hand side starts with $3.3$3.3 but the right hand side already has $6.1$6.1.
needs to be so that both sides of our equation are equal. We do this by looking at what we are doing to one side and changing the other side. We need to look at both numbers though! We can't just add $4.2$4.2 to the right hand side in our equation above, since the left hand side starts with $3.3$3.3 but the right hand side already has $6.1$6.1.
Let's see how we can work through these to find the missing value.
How can we use this?
To see how we can use this in real life, we're going to compare two runners.
![]()
![]()
![]()
In a handicap race, a runner's time is adjusted, to get their adjusted, or handicap, time. We look at two runners and write a statement that means their handicap times are equal. What number do we need to put in to make this true? In Video 2, we look at how to do this, using numbers with tenths and hundredths.
To make our number statement true, we need to make sure both sides are equal. We can look at what is being done to one side, and see what we need to do to the other side.
Sometimes, there is more than one adjustment we need to make.
Worked Examples
Question 1
Complete the equation:
$0.53+0.26=\editable{}+0.56$0.53+0.26=+0.56
Question 2
Complete the equation:
$5.06+2.03=7+\editable{}$5.06+2.03=7+
Question 3
Complete the equation:
$4.124+2.003$4.124+2.003$=$=$\editable{}$$.$.$12$12$+$+$0.007$0.007