Polar Form

A polar coordinate system uses measurements of $r$r, (distance from the origin) and $\theta$θ (angle from the positive horizontal axis called a polar axis).  We use these measurements $r$r,$\theta$θ instead of the cartesian measurements of $x,y$x,y.   Incidently the cartesian coordinates are also referred to as rectangular coordinates (because the cartesian plane is a rectangular plane)

A polar coordinate system therefore looks different to our rectangular coordinate system.  

This is what it looks like. 

 

We can convert our rectangular form of complex numbers $a+bi$a+bi into polar coordinates.  To do so we need the distance from the origin, which is the modulus and the angle from the positive horizontal axis (this is  called the argument).  

Recognising that the horizontal distance $x$x, can be calculated using the angle theta, and similarly for the height $y$y gives us the values of 

$x=r\cos\theta$x=rcosθ

$y=r\sin\theta$y=rsinθ

So we can rewrite the complex number $z=x+iy$z=x+iy as $z=r\cos\theta+ir\sin\theta$z=rcosθ+irsinθ 

We can take $r$r out as a factor so we get $z=r\left(\cos\theta+i\sin\theta\right)$z=r(cosθ+isinθ)

There is special notation for this, a kind of shorthand where we write $\operatorname{cis}$cis to mean $\cos\theta+i\sin\theta$cosθ+isinθ 

 

Having already studied how to find the modulus ($r$r), we just need to identify the value of the argument (the angle) $\theta$θ, and then we can convert rectangular complex numbers $x+iy$x+iy into polar complex numbers $\operatorname{cis}\theta$cisθ

Let's look at this diagram again,   

$\tan\theta=\frac{opposite}{adjacent}=\frac{y}{x}$tanθ=oppositeadjacent​=yx​

The angle is denoted using a number of different notations: $\theta,arg\left(z\right),arg\left(x+iy\right)$θ,arg(z),arg(x+iy)

For $x$x ≠ $0$0, $\tan\theta=y/x$tanθ=y/x

 

The convention for complex numbers is to use radians as the measure for angles.  

Polar form and conguates

Using polar form, if $z=r\operatorname{cis}\left(\theta\right)$z=rcis(θ) then $\overline{z}=r\operatorname{cis}\left(-\theta\right)$z=rcis(−θ)

This is because a complex number has end point coordinate $\left(x,y\right)$(x,y) and the conjugate has coordinate $\left(x,-y\right)$(x,−y).  So the value of the vertical distance from the real axis is identical, the horizontal distance is identical and thus the modulus and argument are identical in size, just that the angle is negative as opposed to positive. 

The conjugate is a reflection of the point on the $x$x-axis in the complex plane. 

Worked examples

Example 1

Write the number $\sqrt{2}-4i$√2−4i in polar form.

To convert to polar form we need the modulus ($r$r) and argument $\left(\theta\right)$(θ)

$r=\sqrt{x^2+y^2}=\sqrt{\left(\sqrt{2}\right)^2+\left(-4\right)^2}=\sqrt{2+16}=\sqrt{18}=4.24$r=√x2+y2=√(√2)2+(−4)2=√2+16=√18=4.24

$\theta=\tan^{-1}\left(\frac{y}{x}\right)=\tan^{-1}\left(\frac{-4}{\sqrt{2}}\right)=1.23$θ=tan−1(yx​)=tan−1(−4√2​)=1.23 radians

So $\sqrt{2}-4i=4.24\operatorname{cis}1.23$√2−4i=4.24cis1.23

 

Example 2

Write the number $6\operatorname{cis}\left(-\frac{2\pi}{3}\right)$6cis(−2π3​) in rectangular form.

Let's draw the number on the plane and mark on $r$r and $\theta$θ.

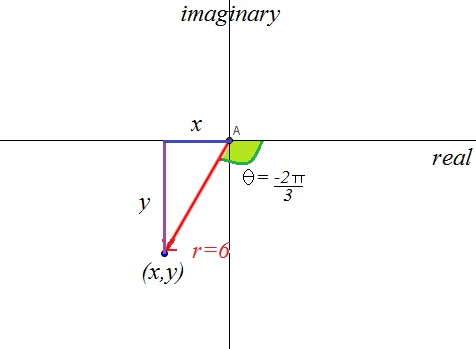
To convert the polar number $6\operatorname{cis}\left(-\frac{2\pi}{3}\right)$6cis(−2π3​) into rectangular form we need to find the values of $x$x and $y$y.  

We can see from the diagram that the angle is $-\frac{2\pi}{3}$−2π3​, so using trigonometry we can find $x$x and $y$y.

$z=r\operatorname{cis}\theta=6\left(\cos\left(\frac{2\pi}{3}\right)+i\sin\left(\frac{2\pi}{3}\right)\right)=6\left(-\cos\left(\frac{\pi}{3}\right)-i\sin\left(\frac{\pi}{3}\right)\right)=6\left(-\frac{1}{2}-i\frac{\sqrt{3}}{2}\right)=-3-3\sqrt{3}i$z=rcisθ=6(cos(2π3​)+isin(2π3​))=6(−cos(π3​)−isin(π3​))=6(−12​−i√32​)=−3−3√3i

 

Just one more thing

There is just one more type of notation, called modulus argument form and it is another way to represent a complex number. We write this as $\left(r,\theta\right)=r\operatorname{cis}\theta$(r,θ)=rcisθ, but you may also see it written as $\left[r,\theta\right]$[r,θ].

A recap of all the new notation:

modulus	distance from the origin
argument (arg)	angle from the positive horizontal axis
$\operatorname{cis}\theta$cisθ	$\cos\theta+i\sin\theta$cosθ+isinθ
modulus argument form	$\left(r,\theta\right)=r\operatorname{cis}\theta$(r,θ)=rcisθ

 

Practice questions

Question 1

Question 2

Question 3

Question 4