How do we know if the calculator is correct? (Investigation)
Checking the calculator. But why?
Why would we need to check the calculator? That's a bit like the computer being wrong. Surely we don't need to check it! Or do we? Where humans (us!) enter any information, there is a chance we could make a mistake. Now. we don't want to work out everything ourselves, as well as using a calculator, but we need to be able to check if an answer is reasonable.
Come and see how Lisa and Larry check their answers, using things they know about multiplication, including doubles and repeated addition, multiplying by 5 or 10, and multiplying by whole numbers.
Activity 1 - checking your multiplication
Before you start, you'll need a calculator and some paper. Draw up 3 columns. In the first column, write down 5 multiplication problems and 5 division problems. You'll see there is a sample below of how it might look. You could use these problems, or choose your own. Some have been filled in already, showing how the estimates were arrived at. Can you find a different way to estimate the answer to those problems? Can you provide closer estimates for any of them?
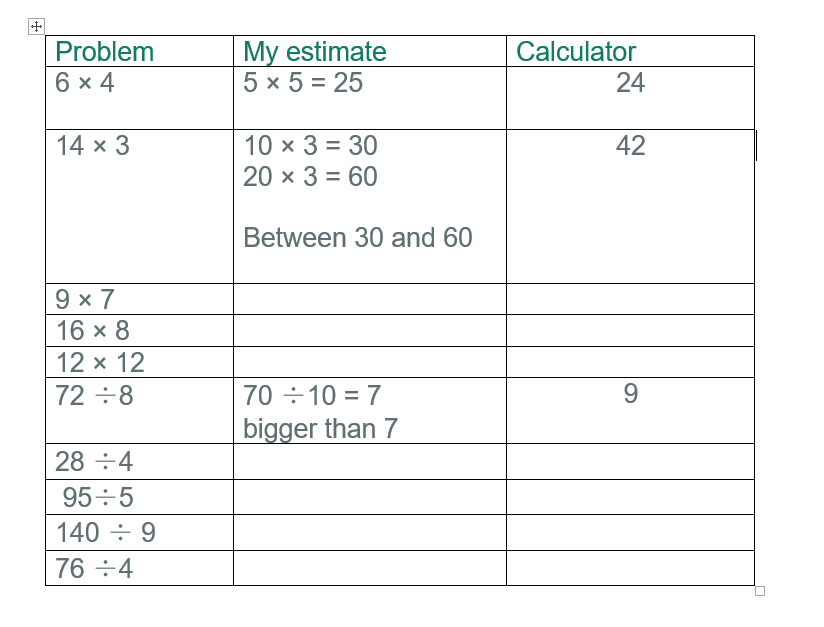
Activity 2 - spotting obvious errors
This time, Lisa and Larry have both used a calculator to solve some problems. Are they correct? While we may not be able to say who is correct by estimating, we can often rule out those that are definitely wrong. Use your estimating skills to see who is definitely wrong, for each problem.
 |
 |
|---|
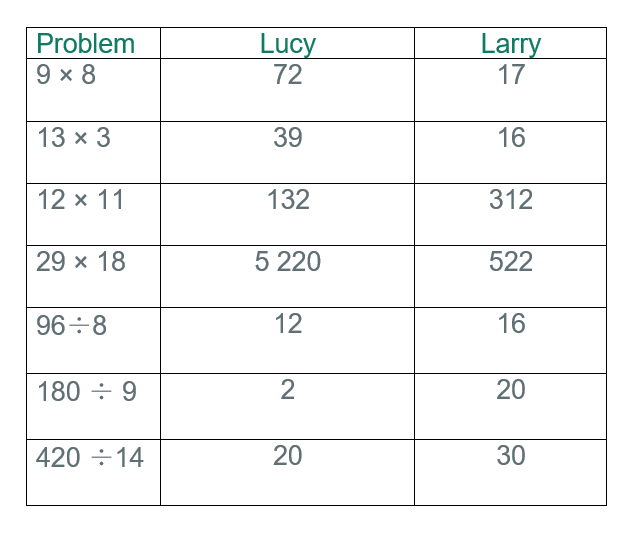
When using a calculator, be sure not to hit the wrong button! If you hit 8 + 9 instead of answer to 8 \times 9, you'll get a very different answer!