Lengths in Quadrilaterals

As we have seen in Types of Quadrilaterals there are specific geometric properties relating to sides and angles that explicitly define certain shapes. 

Some quadrilaterals have specific SIDE properties:

Opposite sides in a parallelogram are parallel   Opposite sides in a parallelogram are equal
Opposite sides in a rectangle are parallel   Opposite sides in a rectangle are equal
All sides of a square are equal   Opposite sides in a square are parallel
Opposite sides in a rhombus are parallel   All sides of a rhombus are equal
1 pair of opposite parallel sides
An isosceles trapezium (trapezoid) has one pair of opposite sides equal   One pair of opposite parallel sides
2 pairs of equal adjacent sides

Diagonals in quadrilaterals

In addition to the properties already studied, the diagonals of some quadrilaterals also have special properties.

Diagonals of a parallelogram bisect each other ($BO=DO$BO=DO &$AO=CO$AO=CO)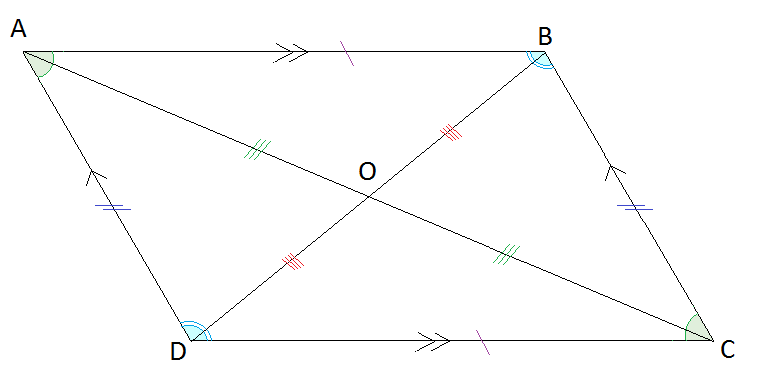
Diagonals of a rectangle bisect each other ($BO=AO$BO=AO= $DO=CO$DO=CO )   Diagonals in a rectangle are equal ($BD=CA$BD=CA)
Diagonals of a square are equal ($AC=BD$AC=BD)   Diagonals of a square bisect each other ($BO=DO$BO=DO = $AO=CO$AO=CO )
Diagonals of a rhombus bisect each other   ($BO=DO$BO=DO and $AO=CO$AO=CO)
The longest diagonal of a kite bisects the shorter diagonal ($BO=OD$BO=OD)
Diagonals of an isosceles trapezium (trapezoid) are equal ($DB=AC$DB=AC)

The following applet will allow you to manipulate different quadrilaterals using the blue points and see the properties appear with regards to the diagonals.  Watch video

Worked Examples

Question 1

ABCD in the adjacent figure is a parallelogram.  Find $x$x and give reasons. 

Question 2

In kite VRTU:

a) Which pairs of sides are equal?

b) Find the size of $\angle VRU$∠VRU, give reasons.