Cointerior Angles
Parallel lines crossed by a transversal
We have already seen how to identify parallel lines, so we can recognise them when they are indicated.
A transversal is a line that crosses a pair of parallel lines.
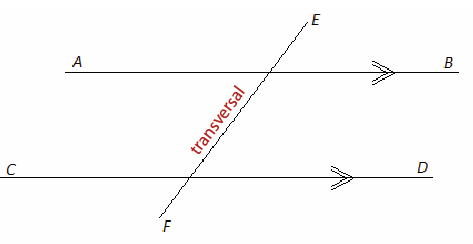 Here, FE is a transversal crossing AB and CD.
Here, FE is a transversal crossing AB and CD.
Cointerior Angles
A pair of angles are said to be cointerior if
- the angles are made from two parallel lines and 1 transversal line (line that crosses the parallel lines)
- the angles are not adjacent (not next to each other)
- the two angles do not share a vertex
- the two angles share a common arm
In these images, angles $a$a and $b$b are cointerior angles, as are $c$c and $d$d.
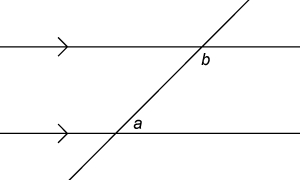
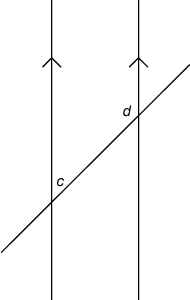
We can use a picture like this to help us remember this rule.
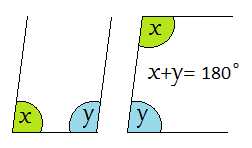
Cointerior angles are supplementary. (add up to 180°)
(To help remember this is sometimes referred to as the U or C rule).
This interactive shows you the relationship between cointerior angles. You can move the parallel lines, and the transversal and see that the cointerior angles are always supplementary (add up to 180). (Watch this video if you would like to see this interactive in action - )
Worked Examples
Question 1
Which of these show a pair of co-interior angles in parallel lines?
Question 2
Are the lines $AB$AB and $CD$CD parallel?
Question 3
Find the values of the pronumerals in the given diagram
a) Find the value of $u$u
b) Find the value of $v$v
Another worked example video coming soon!