Translations
Translations
A translation is what occurs when we move an object or shape from one place to another without changing its size, shape or orientation. Sometimes called a SLIDE, a translation moves every point on an object or shape the same distance in the same direction.
Have a quick play with this interactive. Here you can move the balloon horizontally (left or right) or vertically (up or down). Notice how the balloon does not change shape, it just slides across the page from one place to another.
To identify and describe a translation
- firstly look for corresponding points on the object
- identify if the object has moved horizontally or vertically, and then describe that movement as left/right or up/down
- count the number of places (or units) that the object has moved
Example
Describe the translation from A to B.
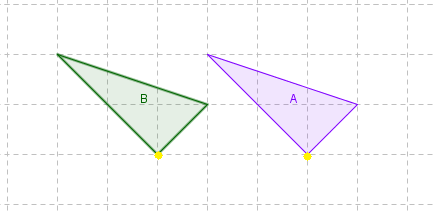
1. Firstly look for corresponding points on the object
- I've highlighted a pair of corresponding points in yellow
2. Identify if the object has moved horizontally or vertically, and then describe that movement as left/right or up/down
- I can see that the shape has a horizontal translation and that from A to B, the object moves left.
3. Count the number of places (or units) that the object has moved
- Counting the units using my corresponding points I can see that it has moved 3 units.
So the translation from A to B is 3 units left.
This applet shows the translation of an object to its image. You can use the sliders to change the horizontal and vertical amounts.
Let's have a look at the following worked solutions.
Question 1
What is the translation from triangle $B$B to triangle $A$A?

$2$2 units left
A$2$2 units right
B$3$3 units left
C$3$3 units right
D
Question 2
What is the translation from square $B$B to square $A$A?
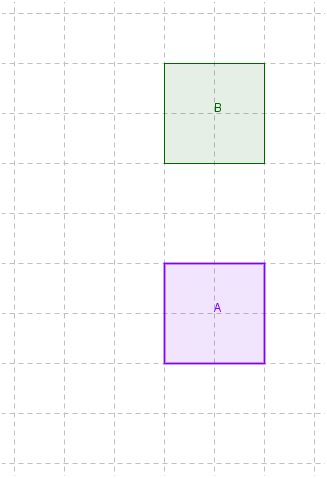
$3$3 units up
A$3$3 units down
B$4$4 units up
C$4$4 units down
D
Question 3
What is the translation from quadrilateral A to quadrilateral B?
$2$2 units left and $4$4 units down
A$4$4 units left and $2$2 units down
B$2$2 units right and $4$4 units up
C$4$4 units right and $2$2 units up
D
