Simple Enlargements
 We've already looked at some different types of transformations we can do to shapes. These are reflections (flips), translations (slides) and rotations (turns). In all these cases, no matter what we do to the shape, it stays the same size.
We've already looked at some different types of transformations we can do to shapes. These are reflections (flips), translations (slides) and rotations (turns). In all these cases, no matter what we do to the shape, it stays the same size.Now we are going to look at some special transformations where we resize our shape, namely enlargements (where we make the shape bigger) and reductions (where we make the shape smaller).
When working out enlargements/ reductions, we need to know the:
- scale factor: how much bigger/ smaller the new shape is than the original shape
- centre of enlargement: where the enlargement is being measured from
For now, we will just focus on scale factor. Watch this video to start!
Scale Factor
As you saw in the video, a scale factor tells us how many times bigger or smaller the new shape is compared to the original. For example, a scale factor of $2$2 means that the sides of the new shape will be twice as long as the original, as shown in the picture below.

Enlargements as Ratios
Scale factors are also commonly written as ratios, e.g. on maps. For example, a ratio of $1:3$1:3 means that for every $1$1 unit of measurement the original shape is, the new object will be $3$3 times longer. For example, if the sides on a square were $5$5 cm long, the new square would have sides $15$15 ($5\times3$5×3) cm long when increased in the ratio $1:3$1:3.
Enlargements as Percentages
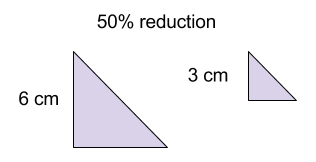
We can also say how much a shape has been enlarged/ reduced as a percentage. It can be helpful to think of the percentage as a fraction to understand what it means. For example, let's say we reduced a triangle by $50%$50%. Remember $50%$50% is the same as $\frac{50}{100}$50100 or $\frac{1}{2}$12, which means the new triangle will be half the size of the original, as shown in the picture below.
Worked Examples
question 1
This horse is next to a centimetre ruler. The scale of the picture to a real horse is $1:20$1:20.

How tall is a real horse from its feet to its ears (in centimetres)?
How tall is the real horse in metres?
Question 2
A square with $2$2cm sides is enlarged by $400%$400%.
How long are the sides on the new square?
Question 3
The green rectangle is an enlargement of the blue rectangle.
What is the enlargement factor?
Write the scale of the blue rectangle to the green rectangle.
$\editable{}:\editable{}$:
