Units of Area Conversions
Converting length
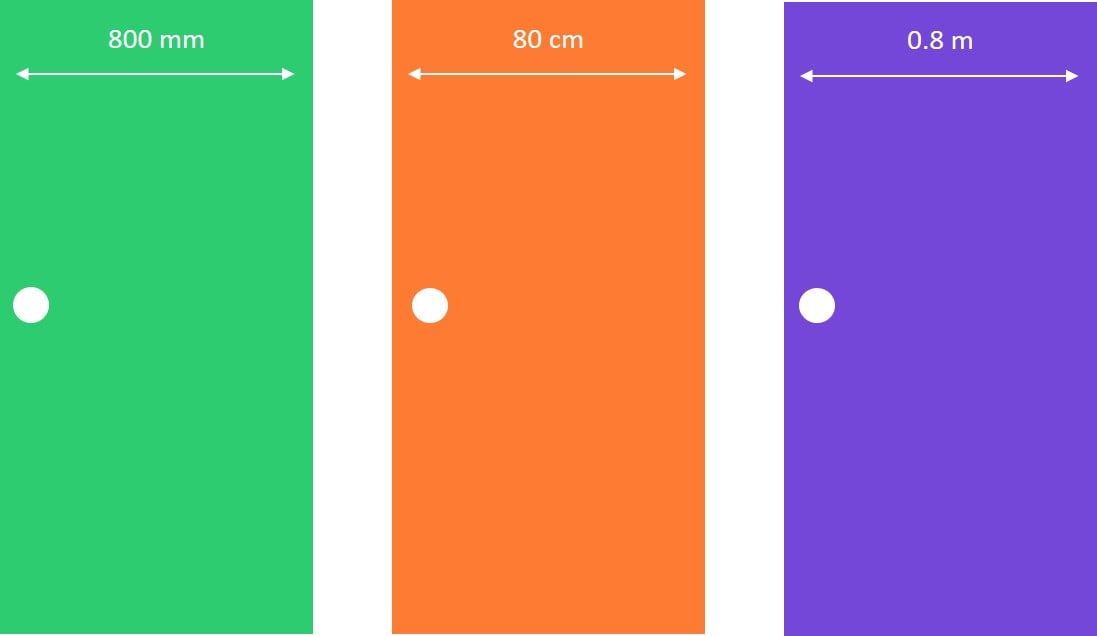
Imagine a door, whose width is 80 cm. This gives us a good idea of how wide it is, but if you buy a door, they are often sold with measurements in millimetres (mm). Knowing how to convert units of length means we can work out the correct width we need. Yes, but what does this have to do with converting units of area?
Now for area
If you need to convert units of area, say, from millimetres (cm) to centimetres (cm), it helps to think of how you'd convert units of length first. To convert area measurements, you need to perform this step twice, because area = length x width. That means converting units of measurement with area can be thought of as the same process as converting length, but with more steps.
Let's see how we can convert units of area, in this video.
Back to our door
Now that we've seen how to convert units of area, we can check which unit of measurement might make sense for the doors. Would you believe that $12800$12800 cm2 is the same area as $1.28$1.28 m2? Don't just take my word for it, watch the video to see how we can prove it.
Worked Example
Question 1
Select the option that shows $3$3 m2 converted into cm2.
$3000$3000 cm2
A$300000$300000 cm2
B$30000$30000 cm2
C$300$300 cm2
D
Decimals
Sometimes we have decimals as our unit of area, such as $0.25$0.25 m2. If we want to express this in whole numbers, we might convert it to cm2, or even mm2. We can use the same steps we've used already, just remembering how we multiply decimals by powers of $10$10.
Worked Example
QUESTION 2
Convert $0.56$0.56km2 to m2.
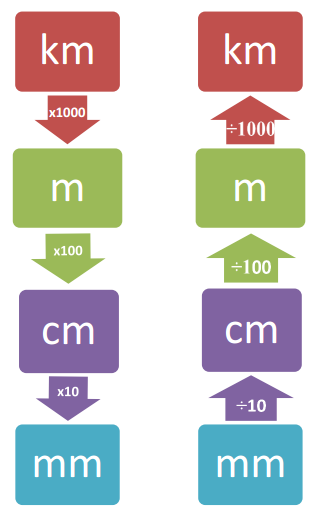
When converting between units of measurement, if we are converting to a smaller unit, such as metres to centimetres, there will be more of the smaller unit, so we use multiplication. If we are converting to a larger unit, such as from centimetres to metres, we'll end up with bigger units, but less of them. That means we use division. This chart can help. Remember though, for area conversions, we need to multiply or divide twice.
Converting even further
So far, we've looked at converting units of area where the units are side by side. What if we need to convert from millimetres (mm) to metres (m), or centimetres (cm) to kilometres (km), for example?
The best part is we do exactly what we have done above, with some extra steps. Let's see how we can do this, and why using a place value chart, or grid paper, might be really useful for recording your answer!
QUESTION 3
Convert $790000000$790000000 cm2 to km2.
Time to play
When converting units of area we need to work out how many smaller square units fit into the larger square unit. This applet can help us to visualise and understand this conversion. Have a look at the different conversions shown here by sliding the slider.
It's always worth checking that you have multiplied (or divided) by the correct amount:
- 10, when converting between mm and cm
- 100, when converting between cm and m
- 1 000, when converting between m and km
It's also important to remember that with area, you multiply (or divide) twice, by these amounts.