10.02 Extension: Perpendiculars and distance
In Algebra 1, you should have become familiar with the standard form of a linear equation: $Ax+By=C$Ax+By=C.
Another form for the equation of a line that is very similar to standard form is called the general form. Essentially it is the same as the standard form, except the constant $C$C now is found on the other side of the equation, and one side has been set equal to zero. General form looks like:
$Ax+By+C=0$Ax+By+C=0
All coefficients $A$A,$B$B and $C$C are integers and the coefficient of $x$x is positive.
We've also studied how to find the distance between two points on a number plane, using the Pythagorean Theorem or the distance formula: $d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$d=√(x2−x1)2+(y2−y1)2.
Perpendicular distance
The perpendicular distance is the shortest distance between a point and a line. The formula for perpendicular distance can be derived from the two formulas reviewed above: General form for the equation of a line, and the distance formula.
Exploration
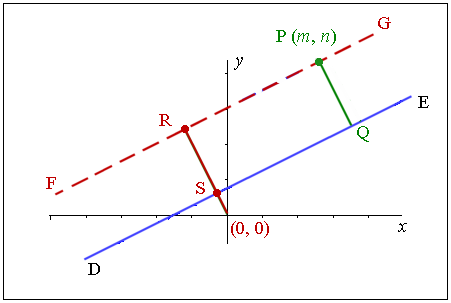
Let's start with the line $Ax+By+C=0$Ax+By+C=0 and label it $\overleftrightarrow{DE}$›‹DE. It has slope of $\frac{-A}{B}$−AB.

Now, let's draw on a point $P$P with coordinates $\left(m,n\right)$(m,n). We want to find the perpendicular distance from the point $P$P to $\overleftrightarrow{DE}$›‹DE (that is, the length $PQ$PQ).

Now, we're going to draw a second line that is parallel to $\overleftrightarrow{DE}$›‹DE (so it has the same slope) and passes through point $P$P. This line has been labeled $\overleftrightarrow{FG}$›‹FG.

Now we will construct another line segment parallel to $\overline{PQ}$PQ that passes through the origin. This line will have slope $\frac{B}{A}$BA because it is perpendicular to $\overleftrightarrow{DE}$›‹DE. Let's call this new length $RS$RS.
We will find the length $RS$RS, which will be the same length $PQ$PQ that we wanted at the start.
Ok, now we've done the prep work, let's do some calculations!
Using the point-slope formula for the equation of a line and rearranging it, we can write the equation of $\overleftrightarrow{FG}$›‹FG as $y=\frac{-Ax+Am+Bn}{B}$y=−Ax+Am+BnB.
Similarly, line $\overleftrightarrow{RS}$›‹RS has the equation $y=\frac{B}{A}x$y=BAx.
Now let's find the point of intersection between $\overleftrightarrow{FG}$›‹FG and $\overleftrightarrow{RS}$›‹RS by using a system of equations.
| $\frac{-Ax+Am+Bn}{B}$−Ax+Am+BnB | $=$= | $\frac{B}{A}x$BAx | (Set the $y$y-values equal to one another) |
| $\frac{A\left(Am+Bn\right)}{A^2+B^2}$A(Am+Bn)A2+B2 | $=$= | $x$x | (Solve for $x$x) |
| $x$x | $=$= | $\frac{A\left(Am+Bn\right)}{A^2+B^2}$A(Am+Bn)A2+B2 | |
| $y$y | $=$= | $\frac{B}{A}\times\frac{A\left(Am+Bn\right)}{A^2+B^2}$BA×A(Am+Bn)A2+B2 | (Substitute into $y=\frac{B}{A}x$y=BAx) |
| $=$= | $\frac{B\left(Am+Bn\right)}{A^2+B^2}$B(Am+Bn)A2+B2 | (Simplify) |
So the coordinates of $R$R are $\left(\frac{A\left(Am+Bn\right)}{A^2+B^2},\frac{B\left(Am+Bn\right)}{A^2+B^2}\right)$(A(Am+Bn)A2+B2,B(Am+Bn)A2+B2).
Using this same process, we can conclude that the coordinates of $S$S are $\left(\frac{-AC}{A^2+B^2},\frac{-BC}{A^2+B^2}\right)$(−ACA2+B2,−BCA2+B2).
Now let's use the distance formula to find $RS$RS:
| $d$d | $=$= | $\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$√(x2−x1)2+(y2−y1)2 |
| $=$= | $\sqrt{\left(\frac{-AC}{A^2+B^2}-\frac{A\left(Am+Bn\right)}{A^2+B^2}\right)^2+\left(\frac{-BC}{A^2+B^2}-\frac{B\left(Am+Bn\right)}{A^2+B^2}\right)^2}$√(−ACA2+B2−A(Am+Bn)A2+B2)2+(−BCA2+B2−B(Am+Bn)A2+B2)2 | |
| $=$= | $\sqrt{\frac{\left(-A\left(Am+Bn+C\right)\right)^2+\left(-B\left(Am+Bn+C\right)\right)^2}{\left(A^2+B^2\right)^2}}$√(−A(Am+Bn+C))2+(−B(Am+Bn+C))2(A2+B2)2 | |
| $=$= | $\sqrt{\frac{\left(A^2+B^2\right)\left(Am+Bn+C\right)^2}{\left(A^2+B^2\right)^2}}$√(A2+B2)(Am+Bn+C)2(A2+B2)2 | |
| $=$= | $\sqrt{\frac{\left(Am+Bn+C\right)^2}{A^2+B^2}}$√(Am+Bn+C)2A2+B2 | |
| $=$= | $\frac{\left|Am+Bn+C\right|}{\sqrt{A^2+B^2}}$|Am+Bn+C|√A2+B2 |
So, the distance from point $\left(x_1,y_1\right)$(x1,y1) to line $Ax+By+C=0$Ax+By+C=0 is given by
$d=\frac{\left|Ax_1+By_1+C\right|}{\sqrt{A^2+B^2}}$d=|Ax1+By1+C|√A2+B2.
The applet below will help visualize that formula:
$d=\frac{\left|Ax_1+By_1+C\right|}{\sqrt{A^2+B^2}}$d=|Ax1+By1+C|√A2+B2
Practice questions
Question 1
Given a point $\left(x_1,y_1\right)$(x1,y1) and a line $Ax+By+C=0$Ax+By+C=0, what formula can we use to find the perpendicular distance $d$d between the point and the line?
$d=\frac{\left|Ax_1+By_1+C\right|}{\sqrt{A^2-B^2}}$d=|Ax1+By1+C|√A2−B2
A$d=\frac{\left|Ax_1+By_1+C\right|}{\sqrt{A^2+B^2}}$d=|Ax1+By1+C|√A2+B2
B$d=\frac{\left|Ax_1-By_1+C\right|}{\sqrt{A^2+B^2}}$d=|Ax1−By1+C|√A2+B2
C$d=\frac{\left|Ax_1-By_1+C\right|}{\sqrt{A^2-B^2}}$d=|Ax1−By1+C|√A2−B2
D
Question 2
Find the perpendicular distance from the origin to the line $4x+7y+5=0$4x+7y+5=0.
Question 3
If the perpendicular distance from the point ($-5$−5, $-1$−1) to the line $-2x-7y+k=0$−2x−7y+k=0 is $\frac{10}{\sqrt{53}}$10√53, what is the value(s) of $k$k?