Class XI

Probability Venn Diagrams - Conditional, Independent and Mutually Exclusive events

Lesson

Let's review our probability laws and apply them to some probability Venn diagrams.

Conditional Probability

Recall that conditional probability occurs when we place conditions on the total number of outcomes and the size of our sample space diminishes.

We can use set notation to expression conditional probability as a rule or relationship.

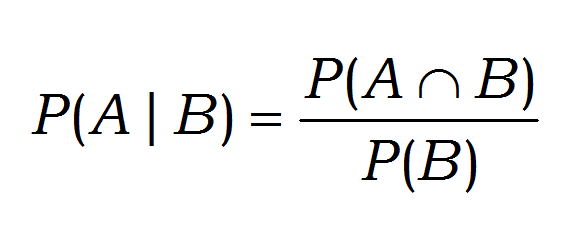
Mutually Exclusive Events

When we say colloquially, or mathematically, that two events are "mutually exclusive" we mean that they have nothing in common.

We can use set notation to express this relationship also.

And by extension of the addition rule we get:

Independent Events

When we talk about events that are independent, we are talking about the fact that one event occurring has no impact on the chances of another event occurring. Each event is independent of the other.

This means that conditional probability doesn't really come into play here. If events $A$A and $B$B are independent, and we know that $B$B has already happened, this will have no bearing on whether $A$A happens.

Thus we can express independent events as:

From the above we can also say:

Example 1:

Use the probability Venn diagram below to calculate the following probabilities.

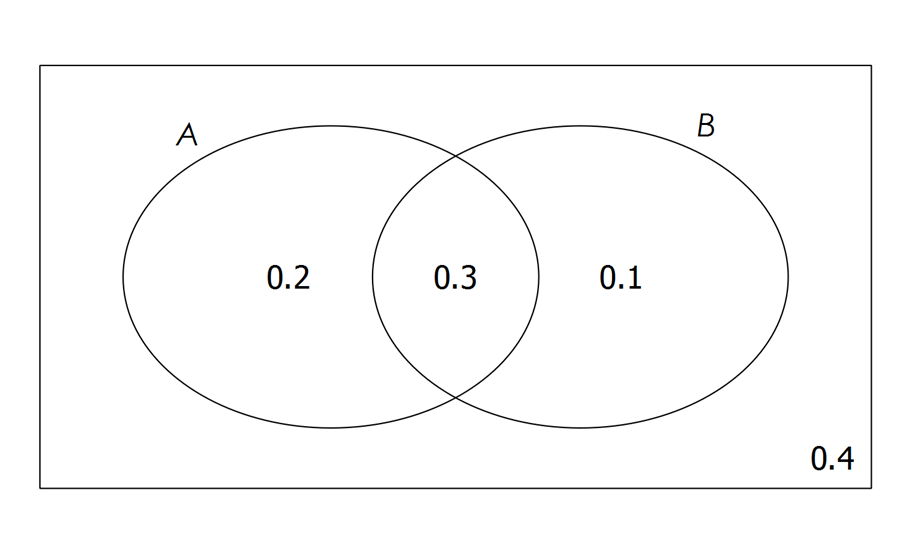
a) $P(A|B)$P(A|B)

b) $P(B|\overline{A})$P(B|A)

Example 2:

Consider events A and B such that:

Are events A and B mutually exclusive?

Think: The easiest way to work this out is to firstly represent this information with a Venn diagram.

Do:

Now we consider the value in the middle region, the intersection, of the Venn diagram. Since all other regions add to $1$1, the intersection will be $0$0. Therefore events A and B are mutually exclusive.

Example 3:

Consider events A and B such that:

Are events A and B independent?

Think: The easiest way to work this out is to firstly represent this information with a Venn diagram.

Do:

Note that we knew the probability of event A using the following calculation.

Now let's use our rule for independence.

Alternatively we could use:

Using either rule we can see that events A and B are not independent.

Worked Examples

Question 1

Consider the following probability Venn diagram:

Calculate the value of $x$x in the diagram. Enter your answer as an equation in $x$x.
Are events $A$A and $B$B mutually exclusive?
Yes
A
No
B

Question 2

Two events $A$A and $B$B are such that:

$P\left(A\cap B\right)=0.02$P(A∩B)=0.02 and $P\left(A\right)=0.2$P(A)=0.2.

If $P\left(B\right)=0.1$P(B)=0.1, are the events $A$A and $B$B independent?
Yes
A
No
B
Are the events $A$A and $B$B mutually exclusive?
Yes
A
No
B

Question 3

Consider the following Venn Diagram.

Find $P$P$($($A\cap B$A∩B$\cap$∩$\overline{C}$C$)$).
Find $P$P$($($\left(A\cup B\right)$(A∪B)$\cap$∩$\overline{C}$C$)$).
Find $P$P$($($B$B$|$|$C$C$)$).
Find $P$P$($($\overline{A}$A$|$|$C$C$)$).
Find $P$P$($($A\cup B$A∪B$|$|$\overline{C}$C$)$).

Outcomes

11.SP.P.1

Random experiments: Outcomes, sample spaces (set representation). Events: Occurrence of events, ‘not’, ‘and’ & ‘or’ events, exhaustive events, mutually exclusive events. Axiomatic (set theoretic) probability, connections with the theories of earlier classes. Probability of an event, probability of ‘not’, ‘and’ & ‘or’ events.