Circles (Mixed and Semi-Circles)

Equation of a Circle with Centre (0,0)
The following interactive allows you to explore the standard form equation of a circle. It shows how the equation changes as the radius $r$r changes. To change the radius, just drag the $r$r slider.
$x^2+y^2=r^2$x2+y2=r2
where $\left(x,y\right)$(x,y) are a pair of coordinates and $r$r is the radius
Proof:
This formula is derived using Pythagoras' theorem. Consider the following graph, which is a circle with the centre at $\left(0,0\right)$(0,0) and a radius of $5$5 units. The blue radius touches the circle at $\left(4,3\right)$(4,3).
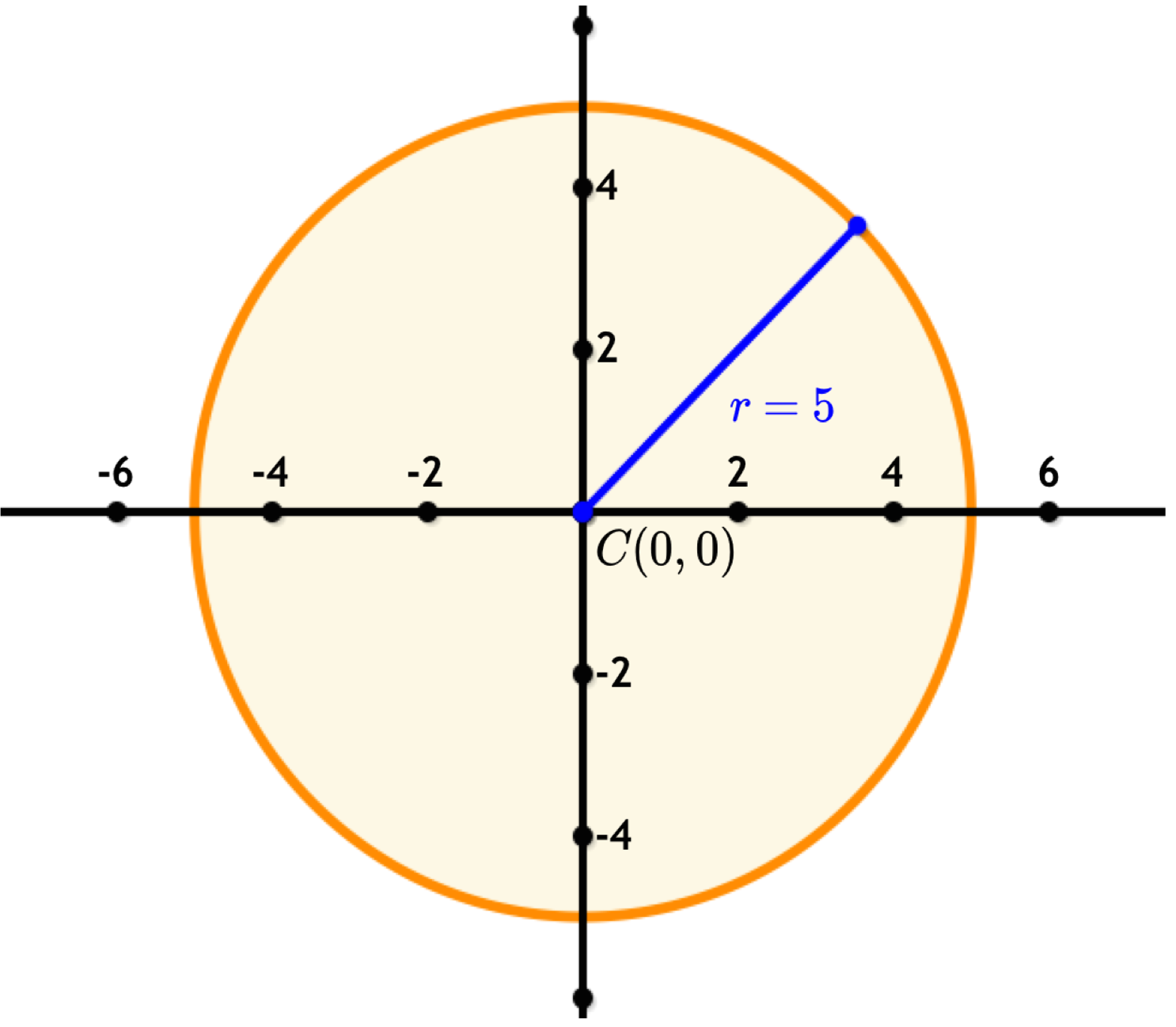
Let's draw in a right-angled triangle:

Using Pythagoras' theorem:
| $3^2+4^2$32+42 | $=$= | $9+16$9+16 |
| $=$= | $25$25 | |
| $=$= | $r^2$r2 |
$\therefore$∴ $x^2+y^2=r^2$x2+y2=r2
Practice Questions
Question 1
State the equation of the circle.
Question 2
Consider the circle $x^2+y^2=4$x2+y2=4.
Find the $x$x-intercepts. Write all solutions on the same line separated by a comma.
Find the $y$y-intercepts. Write all solutions on the same line separated by a comma.
Graph the circle.
Loading Graph...
Vertical Translations
Circles that are centred at the origin have the equation $x^2+y^2=r^2$x2+y2=r2.
Below is a circle with radius $3$3 units that is centred at the origin.

How would the equation change with vertical translations of this circle?
Experimenting with vertical translations
By vertically translating a circle, we are moving it above or below the origin. In the applet below, click and hold the centre of the circle to drag it up and down along the $y$y-axis. You can also move the circle vertically with the $k$k slider, and adjust the radius with the $r$r slider.
Think about the following questions:
- When we change the circle's radius, which part of the equation is affected?
- When we translate the circle vertically, which part of the equation is affected?
- What is the relationship between the $y$y-coordinate of the circle's centre $k$k and the equation?
Equation for vertically translated circles
By using the applet above, we can make the following observations:
- The term on the right side of the equation is always the square of the radius $r$r.
- By translating the circle vertically $k$k units from the origin, its centre has the coordinates $\left(0,k\right)$(0,k).
- $k$k is positive when the circle's centre is above the $x$x-axis and negative when it is below.
- The equation takes the form $x^2+\left(y-k\right)^2=r^2$x2+(y−k)2=r2 with a vertical translation from the origin.
The equation of a circle translated $k$k units vertically from the origin is
$x^2+\left(y-k\right)^2=r^2$x2+(y−k)2=r2,
where $r$r is the radius of the circle.
Practice questions
Question 3
Consider the graph of the circle shown in the Diagram 1.
Loading Graph... |
| Diagram 1 |
The graph of the circle is translated to the position shown in Diagram 2.
Loading Graph...Diagram 2 Which of the following statements is true?
The graph of the circle has been translated $6$6 units up.
AThe graph of the circle has been translated $6$6 units down.
B
Question 4
Which of the following equations describe a circle that has been translated $2$2 units downwards from the origin?
$x^2+\left(y+2\right)^2=r^2$x2+(y+2)2=r2
A$\left(x-2\right)^2+y^2=r^2$(x−2)2+y2=r2
B$\left(x+2\right)^2+y^2=r^2$(x+2)2+y2=r2
C$x^2+\left(y-2\right)^2=r^2$x2+(y−2)2=r2
D
Question 5
Given the graph of $x^2+y^2=6^2$x2+y2=62, draw the graph of $x^2+\left(y+3\right)^2=6^2$x2+(y+3)2=62.
- Loading Graph...
Horizontal Translations
Circles that are centred at the origin have the equation $x^2+y^2=r^2$x2+y2=r2.
Below is a circle with radius $3$3 units that is centred at the origin.

How would the equation change with horizontal translations of this circle?
Experimenting with horizontal translations
By horizontally translating a circle, we are moving it to the left or right of the origin. In the applet below, click and hold the centre of the circle to drag it left and right along the $x$x-axis. You can also move the circle horizontally with the $h$h slider, and adjust the radius with the $r$r slider.
Think about the following questions:
- When we change the circle's radius, which part of the equation is affected?
- When we translate the circle horizontally, which part of the equation is affected?
- What is the relationship between the $x$x-coordinate of the circle's centre $h$h and the equation?
Equation for horizontally translated circles
By using the applet above, we can make the following observations:
- The term on the right side of the equation is always the square of the radius $r$r.
- By translating the circle horizontally $h$h units from the origin, its centre has the coordinates $\left(h,0\right)$(h,0).
- $h$h is positive when the circle's centre is on the right hand side of the $y$y-axis and negative when it is on the left.
- The equation takes the form $\left(x-h\right)^2+y^2=r^2$(x−h)2+y2=r2 with a horizontal translation from the origin.
The equation of a circle translated $h$h units horizontally from the origin is
$\left(x-h\right)^2+y^2=r^2$(x−h)2+y2=r2,
where $r$r is the radius of the circle.
Practice questions
Question 6
Consider the following circles with their respective equations below them.
Loading Graph... |
Loading Graph... |
|
|
|
The graph of $\left(x-2\right)^2+y^2=9$(x−2)2+y2=9 has been horizontally translated from the graph of $x^2+y^2=9$x2+y2=9 by $2$2 units to the:
Left
ARight
B
Question 7
Consider the following circles with their respective equations below them.
Loading Graph... |
Loading Graph... |
|
|
|
The graph of $\left(x+3\right)^2+y^2=4$(x+3)2+y2=4 has been horizontally translated from the graph of $x^2+y^2=4$x2+y2=4 by $3$3 units to the:
Left
ARight
B
Question 8
Consider a circle of radius $3$3 units, centred at the origin. If this circle was horizontally translated $4$4 units to the right of the origin, what would be its equation?
$x^2+\left(y-4\right)^2=9$x2+(y−4)2=9
A$\left(x+4\right)^2+y^2=9$(x+4)2+y2=9
B$x^2+\left(y+4\right)^2=9$x2+(y+4)2=9
C$\left(x-4\right)^2+y^2=9$(x−4)2+y2=9
D
Mixed Translations
Equation of a Circle with any Centre
The following interactive allows you to explore the standard form equation of a circle. It shows how the equation changes as the coordinates of the centre ($h$h, $k$k) and the radius $r$r change. To move the circle, drag the sliders for $h$h and $k$k, the centre coordinates of the circle, while to change the radius, just drag the $r$r slider. You'll notice that, regardless of the values, the equation will always be in the form $\left(x-h\right)^2+\left(y-k\right)^2=r^2$(x−h)2+(y−k)2=r2.
$\left(x-h\right)^2+\left(y-k\right)^2=r^2$(x−h)2+(y−k)2=r2
where $\left(h,k\right)$(h,k) is the coordinates of the centre of the circle
and $r$r is the radius of the circle
The standard form of a circle can also be rearranged and written in general form. The general form of a circle is:
$x^2+y^2+ax+by+c=0$x2+y2+ax+by+c=0
Practice Questions
Question 9
A circle is described by the following equation:
$\left(x+\frac{1}{2}\right)^2+\left(y+\frac{1}{2}\right)^2=\frac{9}{4}$(x+12)2+(y+12)2=94
Find the centre of the circle.
Find the radius of the circle.
Hence sketch the graph for the given circle.
Loading Graph...
Question 10
Consider the circle whose equation is $\left(x+1\right)^2+\left(y+4\right)^2=25$(x+1)2+(y+4)2=25.
State the radius.
State the coordinates of the centre of the circle.
Hence, graph the circle on the coordinate plane below.
Loading Graph...
Semi-circles
We can rewrite the equation of the circle by making $y$y the subject as follows.
| $\left(x-h\right)^2+\left(y-k\right)^2$(x−h)2+(y−k)2 | $=$= | $r^2$r2 | (Writing the equation) |
| $\left(y-k\right)^2$(y−k)2 | $=$= | $r^2-\left(x-h\right)^2$r2−(x−h)2 | (Subtracting by $\left(x-h\right)^2$(x−h)2) |
| $y-k$y−k | $=$= | $\pm\sqrt{r^2-\left(x-h\right)^2}$±√r2−(x−h)2 | (Taking the square root) |
| $y$y | $=$= | $\pm\sqrt{r^2-\left(x-h\right)^2}+k$±√r2−(x−h)2+k | (Adding $k$k) |
We can see that the resulting equation contains two parts:
| $y$y | $=$= | $\sqrt{r^2-\left(x-h\right)^2}+k$√r2−(x−h)2+k | (1) |
| $y$y | $=$= | $-\sqrt{r^2-\left(x-h\right)^2}+k$−√r2−(x−h)2+k | (2) |
We might be curious to find out which sections of the graph represent each part of the equation.
If $x=h$x=h, then:
| $y$y | $=$= | $\sqrt{r^2-\left(x-h\right)^2}+k$√r2−(x−h)2+k | (Writing equation 1) |
| $y$y | $=$= | $\sqrt{r^2-\left(\left(h\right)-h\right)^2}+k$√r2−((h)−h)2+k | (Substituting) |
| $y$y | $=$= | $\sqrt{r^2}+k$√r2+k | (Simplifying the subtraction) |
| $y$y | $=$= | $k+r$k+r | (Simplifying the square root) |
So the graph described by equation (1) contains the top-most point of the circle, $\left(h,k+r\right)$(h,k+r).
If $x=h-r$x=h−r, then:
| $y$y | $=$= | $\sqrt{r^2-\left(x-h\right)^2}+k$√r2−(x−h)2+k | (Writing equation 1) |
| $y$y | $=$= | $\sqrt{r^2-\left(\left(h-r\right)-h\right)^2}+k$√r2−((h−r)−h)2+k | (Substituting) |
| $y$y | $=$= | $\sqrt{r^2-\left(-r\right)^2}+k$√r2−(−r)2+k | (Simplifying the subtraction) |
| $y$y | $=$= | $\sqrt{0}+k$√0+k | (Simplifying the subtraction) |
| $y$y | $=$= | $k$k | (Simplifying the square root) |
So the graph described by equation (1) contains the left-most point of the circle, $\left(h-r,k\right)$(h−r,k). Similarly, we can show that equation (1) also contains the right-most point $\left(h+r,k\right)$(h+r,k) and more generally represents the set of points on the top half of the circle.
 |
| Graph of the equation $y=\sqrt{r^2-\left(x-h\right)^2}+k$y=√r2−(x−h)2+k. |
This implies that the remaining bottom half represents the second equation, $y=-\sqrt{r^2-\left(x-h\right)^2}+k$y=−√r2−(x−h)2+k.
 |
| Graph of the equation $y=-\sqrt{r^2-\left(x-h\right)^2}+k$y=−√r2−(x−h)2+k. |
We call half of a circle a semicircle, and so the two equations $y=\sqrt{r^2-\left(x-h\right)^2}+k$y=√r2−(x−h)2+k and $y=-\sqrt{r^2-\left(x-h\right)^2}+k$y=−√r2−(x−h)2+k represent two semicircles.
The graph of the equation $y=\sqrt{r^2-\left(x-h\right)^2}+k$y=√r2−(x−h)2+k is a semicircle, which represents the top half of the circle centred at $\left(h,k\right)$(h,k) with radius $r$r.
The graph of the equation $y=-\sqrt{r^2-\left(x-h\right)^2}+k$y=−√r2−(x−h)2+k is a semicircle, which represents the bottom half of the circle centred at $\left(h,k\right)$(h,k) with radius $r$r.
Worked example
Consider the semicircle with equation $y=-\sqrt{25-\left(x-10\right)^2}+4$y=−√25−(x−10)2+4.
What is the radius of the semicircle?
Think: The equation of the semicircle is of the form $y=-\sqrt{r^2-\left(x-h\right)^2}+k$y=−√r2−(x−h)2+k where $r$r is the radius.
Do: $r^2=25$r2=25 so the radius is $r=5$r=5.
What is the centre of the semicircle?
Think: The equation of the semicircle is of the form $y=-\sqrt{r^2-\left(x-h\right)^2}+k$y=−√r2−(x−h)2+k where $\left(h,k\right)$(h,k) is the centre.
Do: $h=10$h=10 and $k=4$k=4, so the centre is $\left(10,4\right)$(10,4).
Draw the semicircle.
Think: We first consider the circle centred at $\left(10,4\right)$(10,4) with radius $r=5$r=5. Then we draw only the bottom half to represent the semicircle.
Do:
Reflect: How might the graph of the semicircle change if the equation was $y=\sqrt{25-\left(x-10\right)^2}+4$y=√25−(x−10)2+4?
Practice questions
question 11
The following graph shows a semicircle.
State the centre of the semicircle.
State the radius of the semicircle.
Radius = $\editable{}$ units
Find the equation of this semicircle.
question 12
A certain curve is described by the function $y=-\sqrt{16-x^2}$y=−√16−x2.
What kind of curve is it?
Ellipse
AHyperbola
BParabola
CSemicircle
DState the centre of the semicircle.
State the radius of the semicircle.
Plot the graph for $y=-\sqrt{16-x^2}$y=−√16−x2.
Loading Graph...

