Circles at Origin
We have looked at how to graph different kinds of equations including straight lines, parabolas and hyperbolas. Now we are going to look at how to graph circles whose centres are at the origin.
Equation of a Circle with Centre (0,0)
The following interactive allows you to explore the standard form equation of a circle. It shows how the equation changes as the radius $r$r changes. To change the radius, just drag the $r$r slider.
$x^2+y^2=r^2$x2+y2=r2
where $\left(x,y\right)$(x,y) are a pair of coordinates and $r$r is the radius
Proof:
This formula is derived using Pythagoras' theorem. Consider the following graph, which is a circle with the centre at $\left(0,0\right)$(0,0) and a radius of $5$5 units. The blue radius touches the circle at $\left(4,3\right)$(4,3).
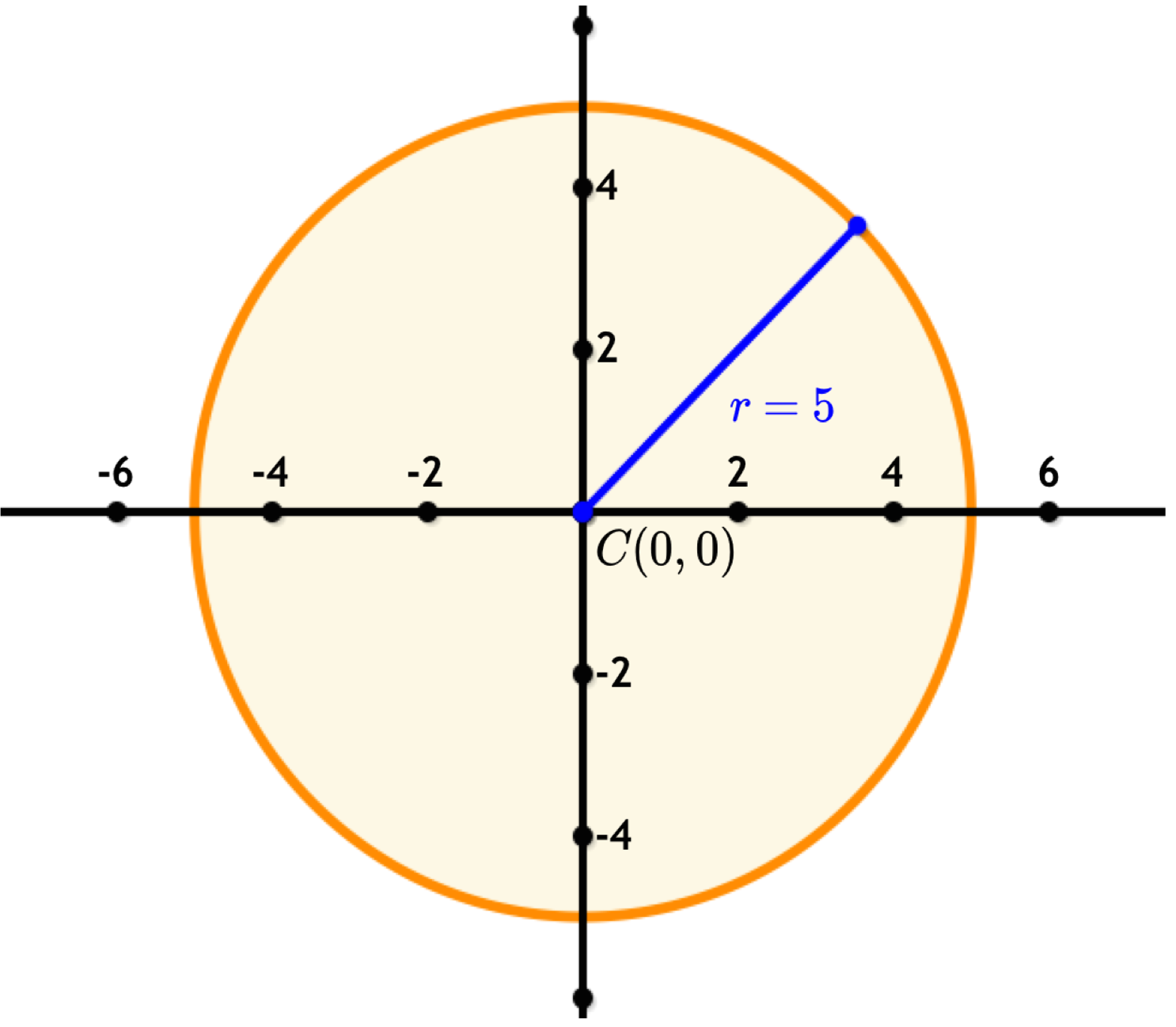
Let's draw in a right-angled triangle:

Using Pythagoras' theorem:
| $3^2+4^2$32+42 | $=$= | $9+16$9+16 |
| $=$= | $25$25 | |
| $=$= | $r^2$r2 |
$\therefore$∴ $x^2+y^2=r^2$x2+y2=r2
Worked Examples
Question 1
State the equation of the circle.
Question 2
Consider the circle $x^2+y^2=4$x2+y2=4.
Find the $x$x-intercepts. Write all solutions on the same line separated by a comma.
Find the $y$y-intercepts. Write all solutions on the same line separated by a comma.
Graph the circle.
Loading Graph...