Cube Root Functions, Transformations and Graphing
Transformations on the basic curve
Just like the square root curve, the transformed cubic root curve given as $y_2=a\sqrt[3]{x-h}+k$y2=a3√x−h+k is the basic function $y_1=\sqrt[3]{x}$y1=3√x dilated by a factor $a$a and translated so that its centre point (at the origin) is relocated to the point $\left(h,k\right)$(h,k).
If $a$a is negative, the basic function is transformed by first reflecting in the $x$x axis, and then dilating and reflecting as before.
Dealing with the switched argument $\left(h-x\right)$(h−x)
One very interesting property of the cubic root function is that the slightly changed form $y_3=a\sqrt[3]{h-x}+k$y3=a3√h−x+k , with the argument switched to $\left(h-x\right)$(h−x), is simply a reflection (across the $x$x axis) of $y_2=a\sqrt[3]{x-h}+k$y2=a3√x−h+k.
This is because:
| $y_3$y3 | $=$= | $a\sqrt[3]{h-x}+k$a3√h−x+k |
| $=$= | $a\sqrt[3]{-\left(h-x\right)}+k$a3√−(h−x)+k | |
| $=$= | $a\times\sqrt[3]{-1}\sqrt[3]{\left(h-x\right)}+k$a×3√−13√(h−x)+k | |
| $=$= | $a\times\left(-1\right)\sqrt[3]{\left(h-x\right)}+k$a×(−1)3√(h−x)+k | |
| $=$= | $-a\sqrt[3]{\left(h-x\right)}+k$−a3√(h−x)+k | |
| $=$= | $-y_2$−y2 |
Note that if $y_2$y2 has a negative dilation factor, then $y_3$y3 will be a reflection of an already reflected curve.
To emphasise this point, the curve $y=2\sqrt[3]{\left(3-x\right)}+5$y=23√(3−x)+5 is identical to the curve $y=-2\sqrt[3]{\left(x-3\right)}+5$y=−23√(x−3)+5, and the curve $y=-2\sqrt[3]{\left(x-3\right)}+5$y=−23√(x−3)+5 is identical to the curve $y=2\sqrt[3]{\left(3-x\right)}+5$y=23√(3−x)+5.
That is, if you wish to switch the argument from $\left(h-x\right)$(h−x) to $\left(x-h\right)$(x−h), or vice versa, you must change the sign of the dilation factor.
A typical cube root function
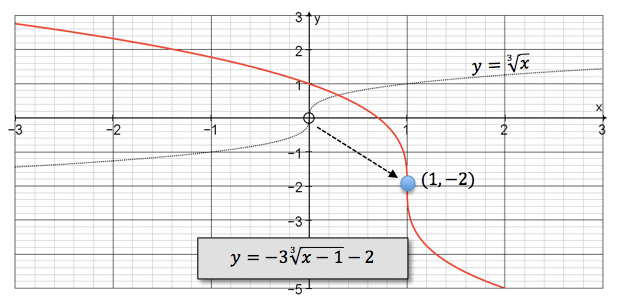
Here is the graph of $y=-3\sqrt[3]{x-1}-2$y=−33√x−1−2. The grey curve shows the basic cube root function $y=\sqrt[3]{x}$y=3√x .
The Applets
The first applet allows you to vary the dilation factor and the translation constants $h$h and $k$k. Make sure you look at the full range of possibilities - in particular negative values of $a$a.
Applet 1
This second applet gives you the opportunity to compare two different transformed cube root functions - one with the argument under the cube root sign given as $\left(x-h\right)$(x−h) and one with the argument as $\left(h-x\right)$(h−x). Choose different values for the dilation factors and translation constants.
In particular, satisfy yourself that $y=2\sqrt[3]{\left(3-x\right)}+5$y=23√(3−x)+5 is identical to $y=-2\sqrt[3]{\left(x-3\right)}+5$y=−23√(x−3)+5 and that $y=-2\sqrt[3]{\left(x-3\right)}+5$y=−23√(x−3)+5 is identical to $y=2\sqrt[3]{\left(3-x\right)}+5$y=23√(3−x)+5.
Applet 2
Worked Examples
QUESTION 1
Consider the function $f\left(x\right)=\sqrt[3]{x}$f(x)=3√x.
Complete the table of values below:
$x$x $-8$−8 $-1$−1 $0$0 $1$1 $8$8 $\sqrt[3]{x}$3√x $-2$−2 $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Now draw a graph of the function, making sure to include the point of symmetry.
Loading Graph...What is the domain of the function?
$x>0$x>0
AAll real numbers.
B$x\le0$x≤0
C$x\ge0$x≥0
DWhat is the range of the function?
All real numbers.
A$y\le0$y≤0
B$y>0$y>0
C$y\ge0$y≥0
D
QUESTION 2
Consider the function $f\left(x\right)=\sqrt[3]{x-1}+4$f(x)=3√x−1+4.
Which of the following are points that lie on the graphed function? Select the two that apply.
$\left(1,0\right)$(1,0)
A$\left(0,4\right)$(0,4)
B$\left(2,-6\right)$(2,−6)
C$\left(1,4\right)$(1,4)
D$\left(2,5\right)$(2,5)
EGraph the curve.
Loading Graph...What is the domain?
$x\ge4$x≥4
AAll real numbers.
B$x\ge0$x≥0
C$x\ge1$x≥1
DWhat is the range?
$y\ge0$y≥0
A$y\ge1$y≥1
B$y\ge4$y≥4
CAll real numbers.
D