
Volume of Composite Solids (prisms and cylinders)
Composite solids are just a combination of simpler solids in disguise.
To find the volume of composite solids such as these:
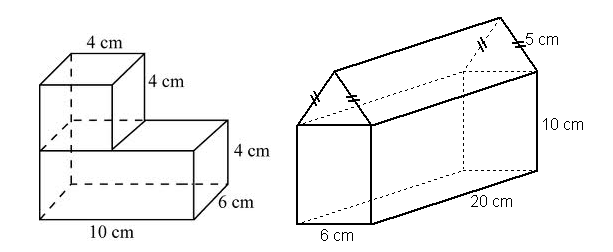
- break down the shape into smaller and simpler solids
- find the volume of the individual smaller solids
- add up the volumes of the individual solids to find the total volume
The exception to these steps is when the solid we are looking at is more simply considered as a larger solid with a smaller solid cut out of it, like these ones.
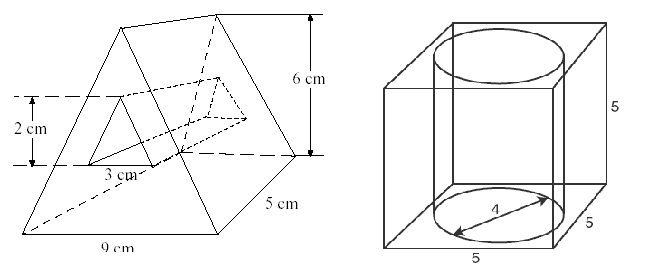
In this case we would
- identify the large solid as well as the solid that has been cut out of it
- find the volume of both pieces
- subtract the volume of the cut out piece from the volume of the larger piece
Now we can look at many different composite solids and consider them in terms of all the solids we know.

$\text{Volume of Prisms }=\text{Area of Base }\times\text{Height of Prism }$Volume of Prisms =Area of Base ×Height of Prism
$\text{Volume of Cube }=s^3$Volume of Cube =s3
$\text{Volume of Rectangular Prism }=lwh$Volume of Rectangular Prism =lwh
$\text{Volume of Cylinder }=\pi r^2h$Volume of Cylinder =πr2h
$\text{Volume of Right Pyramid }=\frac{1}{3}\times\text{Base Area}\times\text{Height of Pyramid}$Volume of Right Pyramid =13×Base Area×Height of Pyramid
$\text{Volume of Right Cone }=\frac{1}{3}\pi r^2h$Volume of Right Cone =13πr2h
$\text{Volume of Sphere }=\frac{4}{3}\pi r^3$Volume of Sphere =43πr3
Worked Examples
Question 1
Question 2
Find the volume of the figure shown, correct to two decimal places.
