Convert from decimals to fractions
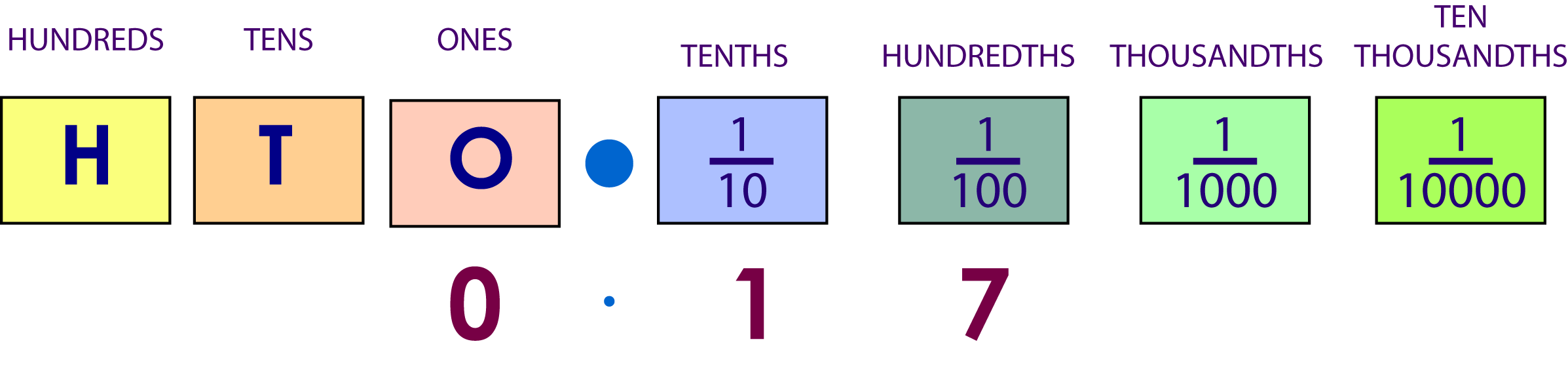
The decimal I have written in the place value table is $0.17$0.17. You can see that the last number I've written is in the hundredths column, so the denominator (bottom number) of our fraction is $100$100. As a fraction, we would write this as $\frac{17}{100}$17100.
Examples
question 1
Evaluate: Express $0.4$0.4 as a fraction in its simplest form.
Think: This decimal finishes in the tenths column
Do: $\frac{4}{10}$410= $\frac{2}{5}$25
We can convert any decimal in the same way!
Question 2
Evaluate: Express $0.08$0.08 as a fraction in its simplest form.
Think: This decimal finishes in the hundredths column
Do: $\frac{8}{100}$8100= $\frac{2}{25}$225
question 3
Evaluate: Express $0.155$0.155 as a fraction in its simplest form.
Think: This decimal finishes in the thousandths column
Do: $\frac{155}{1000}$1551000 = $\frac{31}{200}$31200
Mixed numbers
Just keep on using the same pattern when you are writing numbers with decimals as a mixed number.
Remember- the number to the left of the decimal point does not have to change.
Examples
question 4
Evaluate: Convert $5.12$5.12 to a mixed number
Think: The $5$5 is a whole number and the decimal finishes in the hundredths column
Do: $5\frac{12}{100}=5\frac{3}{25}$512100=5325
Question 5
Evaluate: Convert $17.1$17.1 to a mixed number
Think: The $17$17 is a whole number and the decimal finishes in the tenths column
Do: $17\frac{1}{10}$17110
Expressing decimals as the sum of integers and fractions
This may sound a bit fancy but really it just means "write each number according to its place value and then write all the numbers as an addition." You have already done this with whole numbers, so let's look at some examples with decimals. These questions normally say we don't need to simplify the fractions.
Examples
question 6
Evaluate: Express $18.97$18.97 as the sum of integers and fractions. Fractions do not need to be simplified.
Think: Remember the place value of each number.
Do: $10+8+\frac{9}{10}+\frac{7}{100}$10+8+910+7100
Question 7
Evaluate: Express $0.482$0.482 as the sum of integers and fractions. Fractions do not need to be simplified.
Think: Remember the place value of each number.
Do: $\frac{4}{10}+\frac{8}{100}+\frac{2}{1000}$410+8100+21000
More Worked Examples
Question 1
Write the decimal $0.2$0.2 as a fraction in its simplest form.
Question 2
Write the decimal $0.26$0.26 as a fraction in its simplest form.
Question 3
Write the decimal $1.856$1.856 as a simplified improper fraction.
Question 4
Express the following as the sum of integers and fractions that show the place value of each digit: $1.416$1.416
Fractions need not be simplified. For example: $23.5=20+3+\frac{5}{10}$23.5=20+3+510