Convert thousandths between fractions and decimals
We've already looked at decimals, which are parts of a whole. Up until now, we have only looked at decimals less than one. Now we are going to look at values with whole numbers and decimals.
Writing numbers with Decimals
Let's look at the place value table.

When we wrote a number less than one (e.g. $17$17 hundredths or $0.17$0.17), we were actually filling in the place value table like so:
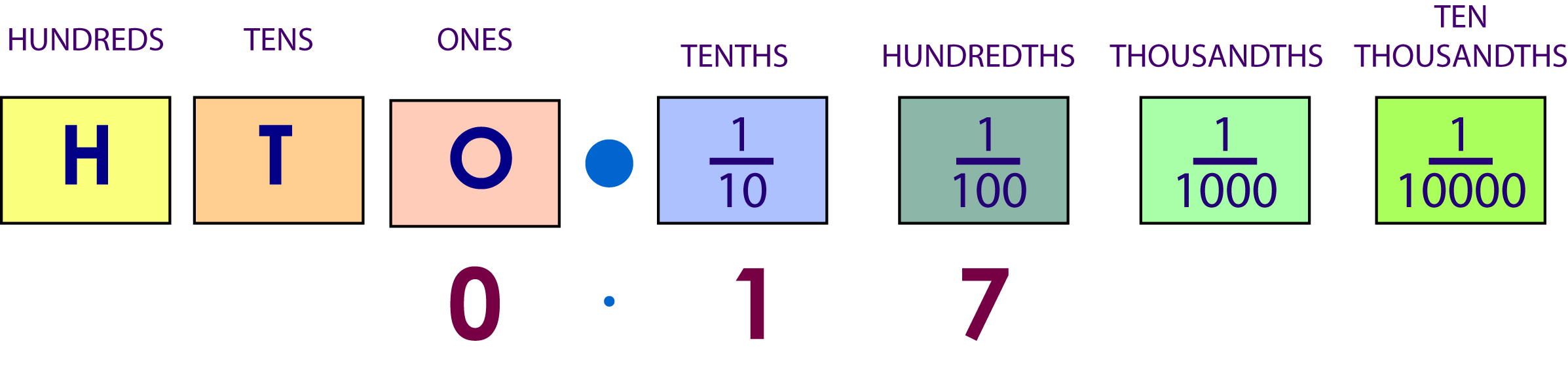
The same thing happens when we write a number with wholes and a decimal. For example, if I had $23$23 wholes and $47$47 hundredths, I would write it as $23.47$23.47, which in the place value table looks like:

The applet below shows a part of a shaded block. Try changing how much of each block is shaded and see how that would change the value of the decimal.
Where do numbers with decimals fit on the number line?
Numbers with decimals fit in between whole numbers on a number line. For example $1.5$1.5 would be between $1$1 and $2$2. Just like with whole numbers, the bigger the decimal, the further up the number line it will be.
You can look at how decimals fit on the number line using the applet below.
Worked examples
Question 1
Complete the following:
$9.12$9.12 = $\editable{}$ unit(s), $\editable{}$ tenth(s), and $\editable{}$ hundredth(s).
Question 2
Select either $>$> or $<$< to complete the following:
| $9.965$9.965 | ___ | $9.964$9.964 |
|---|
$<$<
A$>$>
B
Question 3
Write the fraction $\frac{6696}{1000}$66961000 as a decimal.