Estimate and Compare Angles

Estimation

One skill we really need to develop is the ability to estimate angles.  Like all estimation, getting good at it just takes practice, but we can use some simple benchmarks to narrow down the values.  

Good benchmarks to use for angles are $90^\circ$90° and $180^\circ$180°.

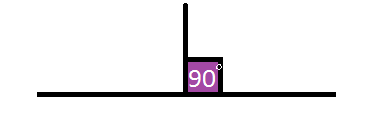
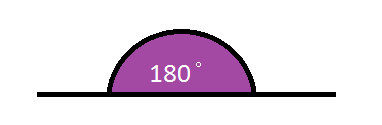
So angles like these could be easily estimated to be around $90^\circ$90° and $180^\circ$180°.

   

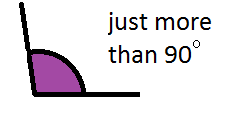
Reasonable estimates for the above might be around $95^\circ$95° and $170^\circ$170°.  

Also angles that are midway between these such as  $45^\circ$45° (half of $90^\circ$90°) and $135^\circ$135° (halfway between $90^\circ$90° and $180^\circ$180°) can be useful benchmarks. 

 

Measuring

If we need to be more accurate, we would need to measure the angle.  Just like how we measure a line with a ruler or tape measure, we can measure an angle using a special tool called a protractor. 

A protractor looks like this, and has two rows of numbers.  This allows us to measure angles going in either the clockwise, or anticlockwise direction. 

To use a protractor we follow these steps.

Line up the horizontal base line on the protractor with one of the arms of the angle, at the same time place the centre crosshairs of the protractor on the vertex of the angle

Identify which row of numbers (outer or inner) starts at $0$0 on the arm of the angle. (for us in the image above the inner row of numbers is what we need)

Then measure the value of the angle by identifying the number the other arm of the angle passes through.

Our angle is $124^\circ$124°

 

Now it's your turn, this applet will let you practice measuring angles with a protractor.  Why not also try and estimate the angle first - remember practice makes perfect!

 

 

Making angles

You may have just discovered using the applet above that it also lets you make angles.  If you didn't play with that part before, do it now.  If you need some pointers on how to make the angles read on...

• one arm of the angle has to be on the ZERO line of the protractor
• the other arm is then moved until the correct angle is reached
• make sure you are reading of the correct numbers (either outer or inner), depending on where the zero arm is

 

Examples

Question 1

Which angle is bigger?

A)                B) 

Think: The angle in (A) is less than $90^\circ$90°. The angle in (B) is more than $90^\circ$90°. 

Do: B is the bigger angle.

 

Question 2

Estimate the size of the angle marked in yellow.

Think: $90^\circ$90° is a right angle. This angle is approximately halfway between $0^\circ$0° and $90^\circ$90°.

Do: This angle is approximately $45^\circ$45°.

Worked Examples

QUESTION 3

QUESTION 4

QUESTION 5