We've looked at quadratics and how we can graph them as parabolas. We also looked at groups of different features of these quadratics, including concavity, turning points, intercepts, slope, as well as their symmetrical shape.
In this chapter, we are going to look more at turning points. A quadratic will have either a minimum or a maximum value at its turning point.
Maximum and Minimum Values
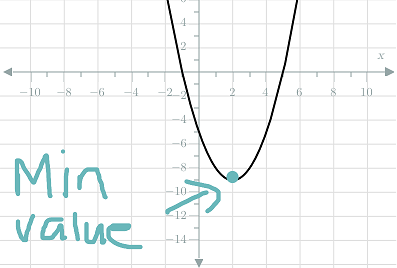
Parabolas that are concave up have a minimum value. This means their $y$y value will never be less than a certain value.
Similarly, parabolas that are concave down have a maximum value. This means their $y$y value will never be more than a certain value.
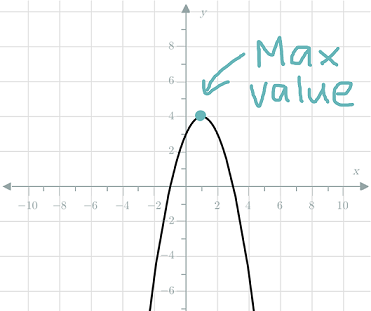
The minimum or maximum value always occurs at the axis of symmetry.
Finding the Equation of the Axis of Symmetry
It's easy to see a maximum and minimum values when we look at graphs. However, we can also find these minimum or maximum values algebraically. To do this, we need to find the axis of symmetry
$x=\frac{-b}{2a}$x=−b2a
Remember, the general form of a quadratic is $y=ax^2+bx+c$y=ax2+bx+c, so we just need to substitute in the relevant values. For example, let's find the equation of the axis of symmetry for $y=2x^2-4x+7$y=2x2−4x+7.
In this example, $a=2$a=2 and $b=-4$b=−4, so let's substitute them into the formula:
| $x$x | $=$= | $\frac{-\left(-4\right)}{2\times2}$−(−4)2×2 |
| $=$= | $\frac{4}{4}$44 | |
| $\therefore$∴ $x$x | $=$= | $1$1 |
Finding the Turning Point
- Determine whether the parabola is concave up or down. This will tell us whether we're finding a minimum or maximum value.
- Find the $x$x value of the turning point using the axis of symmetry formula.
- Substitute the value from step 2 into the original equation to find the $y$y value.
Examples
Question 1
Consider the equation $y=2x^2$y=2x2.
Is every value of $y$y positive?
No
AYes
BThe graph of $y=2x^2$y=2x2 is given below.
Loading Graph...State the axis of symmetry of the parabola.
What is the minimum value of $y$y?
$y$y$=$=$\editable{}$
Question 2
Consider the curve $y=2\left(x-3\right)^2+3$y=2(x−3)2+3.
Is the graph of the curve concave up or concave down?
Concave up
AConcave down
BWhat is the axis of symmetry of the parabola?
What is the minimum value of the graph?
$y$y$=$=$\editable{}$
At which value of $x$x does the minimum value occur?
$x$x $=$= $\editable{}$
If the graph was shifted $4$4 units downwards, what would be the new minimum value?
Question 3
Consider the equation $y=\left(x-12\right)\left(x-6\right)$y=(x−12)(x−6)
State the zeros of the function on the same line, separated by a comma.
Find the axis of symmetry.
The graph of the function is:
Concave up
AConcave down
BThe graph has a:
Maximum value
AMinimum value
BDetermine the minimum $y$y value of the function.