Let's explore how a quadratic function changes using the applet below. What happens when we change the sliders for dilation, reflection, vertical translation and horizontal translation? Can you describe what changes these values make to the quadratic function?
These movements are called transformations. Transform means change, and these transformations change the simple quadratic $y=x^2$y=x2 into other quadratics by moving (translating), flipping (reflecting) and making the graph appear more or less steep (dilating).
By using the above applet, step through these instructions:
- Start with the simple quadratic $y=x^2$y=x2
- Dilate the quadratic by factor of $2$2
- Reflect on the $x$x-axis
- Translate vertically by $2$2 and horizontally by $-3$−3 units
How has the graph changed? Can you visualise the changes without using the applet? What is the resulting equation?
Equations and Transformations of Quadratics
Transforming a quadratic will change its equation. Here are some of the most common types of quadratic equations, and what they mean with regards to the transformations that have occurred.
$y=ax^2$y=ax2
If $a<0$a<0 (that is, $a$a is negative) then we have a reflection parallel to the $x$x-axis. It's like the quadratic has been flipped upside down.
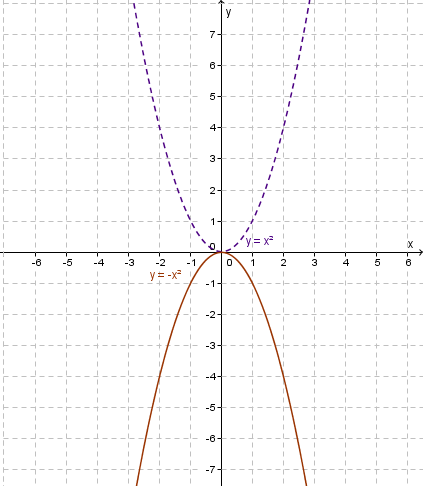
Shows the reflection of
$y=x^2$y=x2 to $y=-x^2$y=−x2
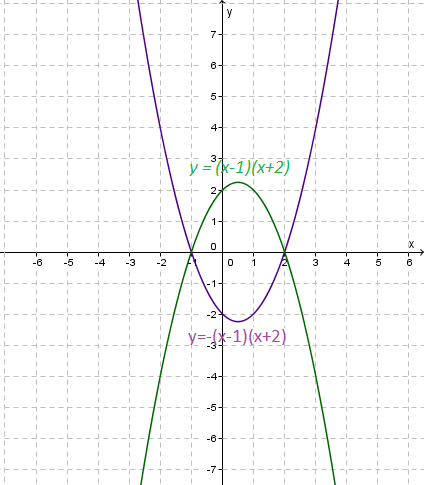
Shows the reflection of
$y=\left(x-1\right)\left(x+2\right)$y=(x−1)(x+2) to $y=-\left(x-1\right)\left(x+2\right)$y=−(x−1)(x+2)
$y=ax^2$y=ax2
This is a quadratic that has been dilated vertically by a factor of $a$a.
If $\left|a\right|>1$|a|>1 then the graph is steeper than $y=x^2$y=x2.
If $\left|a\right|<1$|a|<1 then the graph is flatter than $y=x^2$y=x2.
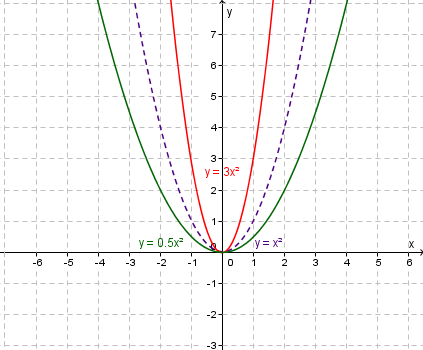
Dilation of $y=x^2$y=x2 to $y=3x^2$y=3x2 and $y=\frac{1}{2}x^2$y=12x2
$y=ax^2+k$y=ax2+k
In the graph $y=ax^2+k$y=ax2+k, the quadratic has been vertically translated by $k$k units.
If $k>0$k>0 then the translation is up.
If $k<0$k<0 then the translation is down.
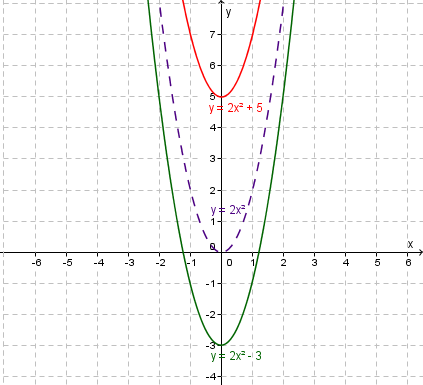
Vertical translation.
Showing one curve $y=2x^2+5$y=2x2+5 having a vertical translation of up $5$5 units, and
another $y=2x^2-3$y=2x2−3 having a vertical translation of down $3$3 units.
$y=\left(x-h\right)^2$y=(x−h)2
The $h$h indicates the horizontal translation.
If $h>0$h>0, that is the factor in the brackets is $\left(x-h\right)$(x−h) than we have a horizontal translation of $h$h units right.
If $h<0$h<0, that is the factor in the brackets is $\left(x-\left(-h\right)\right)=\left(x+h\right)$(x−(−h))=(x+h) than we have a horizontal translations of $h$h units left.
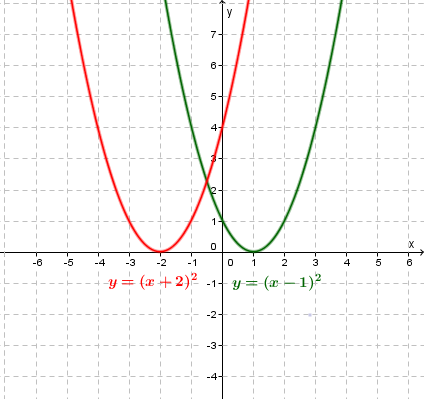
The graph $y=x^2$y=x2 being horizontally translated $2$2 units left
to $y=\left(x+2\right)^2$y=(x+2)2 and $1$1 unit right to $y=\left(x-1\right)^2$y=(x−1)2
The Turning Point
The turning point of a quadratic is the point where the function turns. This point is also known as the vertex of the parabola.
It changes from being decreasing to increasing, like in this positive quadratic.

Or changes from being increasing to decreasing, like in this negative quadratic.

Turning Point Form
The form $y=a\left(x-h\right)^2+k$y=a(x−h)2+k is called turning point form. It's really useful for two reasons:
- It tells us the turning point immediately, and knowing the turning point we can draw a pretty good sketch of any quadratic.
- It explains to us a number of transformations that have occurred to the quadratic from the simple quadratic $y=x^2$y=x2.
Identifying transformations
The form $y=a\left(x-h\right)^2+k$y=a(x−h)2+k shows us:
Vertical Dilation a
If $\left|a\right|>1$|a|>1 then the quadratic is steeper than $x^2$x2.
If $\left|a\right|<1$|a|<1 then the quadratic is flatter than $x^2$x2.
Reflection a
If $a<0$a<0 then the quadratic is a reflection of $ax^2$ax2 on a line parallel to the $x$x-axis.
Vertical Translation k
If $k>0$k>0 then the translation is up.
If $k<0$k<0 then the translation is down.
Horizontal Translation h
If $h<0$h<0 then the translation is to the left, and $x+h$x+h appears in the brackets.
If $h>0$h>0 then the translation is to the right, and $x-h$x−h appears in the brackets.
Examples
Question 1
The function $y=-5x^2$y=−5x2 has what dilation factor?
Dilation factor $=$= $\editable{}$
Question 2
The quadratic $y=x^2$y=x2 has been transformed into $y=3\left(x-4\right)^2$y=3(x−4)2. Has there been a reflection?
Yes, across the $x$x-axis
AYes, across the $y$y-axis
BNo$\text{ }$
C
Question 3
The quadratic $y=x^2$y=x2 has been transformed into $y=-4\left(x+10\right)^2$y=−4(x+10)2. Identify the vertical translation.
$0$0 units up or down
A$4$4 units up
B$10$10 units down
C$10$10 units up
D
Question 4
The quadratic $y=x^2$y=x2 has been transformed into the following graph:
What is the vertical translation?
$4$4 units up
A$4$4 units down
B$3$3 units down
C$3$3 units up
DWhat is the horizontal translation?
$3$3 units right
A$4$4 units left
B$3$3 units left
C$4$4 units right
DHas the curve been reflected about the $x$x-axis?
No
AYes
BHas this quadratic had a change in dilation from the standard $y=x^2$y=x2 curve?
Yes
ANo
B