Reading and Interpreting Time Series Graphs
Time Series data refers to bivariate data where the explanatory variable, or independent variable, is time. This can be time in hours, days, months, weeks, quarters or any unit of time.
The response or dependent variable can be a range of contexts and most often they are seasonal in nature.
Some examples of time series data include:
- fuel prices - they tend to rise and fall in a cyclical pattern according to the day of the week
- airconditioner sales - they do not remain constant all year, but sales increase and decrease according to the time of year
- ocean tides - their height is cyclical over a 24 hour period
Graphs and Language of Time Series Data
When we examine a graph of time series data, there are many noteworthy features.
Trend - by looking at the graph we can see overall whether the response variable is increasing (positive trend) or decreasing (negative trend).
Seasonality - by following the rise and fall, or cyclical nature of the data, we can determine how many seasons or time periods constitute one cycle of the data. This will be helpful to us later on.
Irregular Fluctuations - once we've observed the first two, we'll be interested to see whether the data for some seasons or for entire cycles are experiencing irregular fluctuations and unexpected results.
Outliers - also by observing the trends and seasonality we will easily be able to spot an outlier.
Let's take a look at a few time series graphs.
Example 1
The following graph is from the data collected by the Australian Competition and Consumer Commission and represents the fuel price cycle for Perth in early 2016.
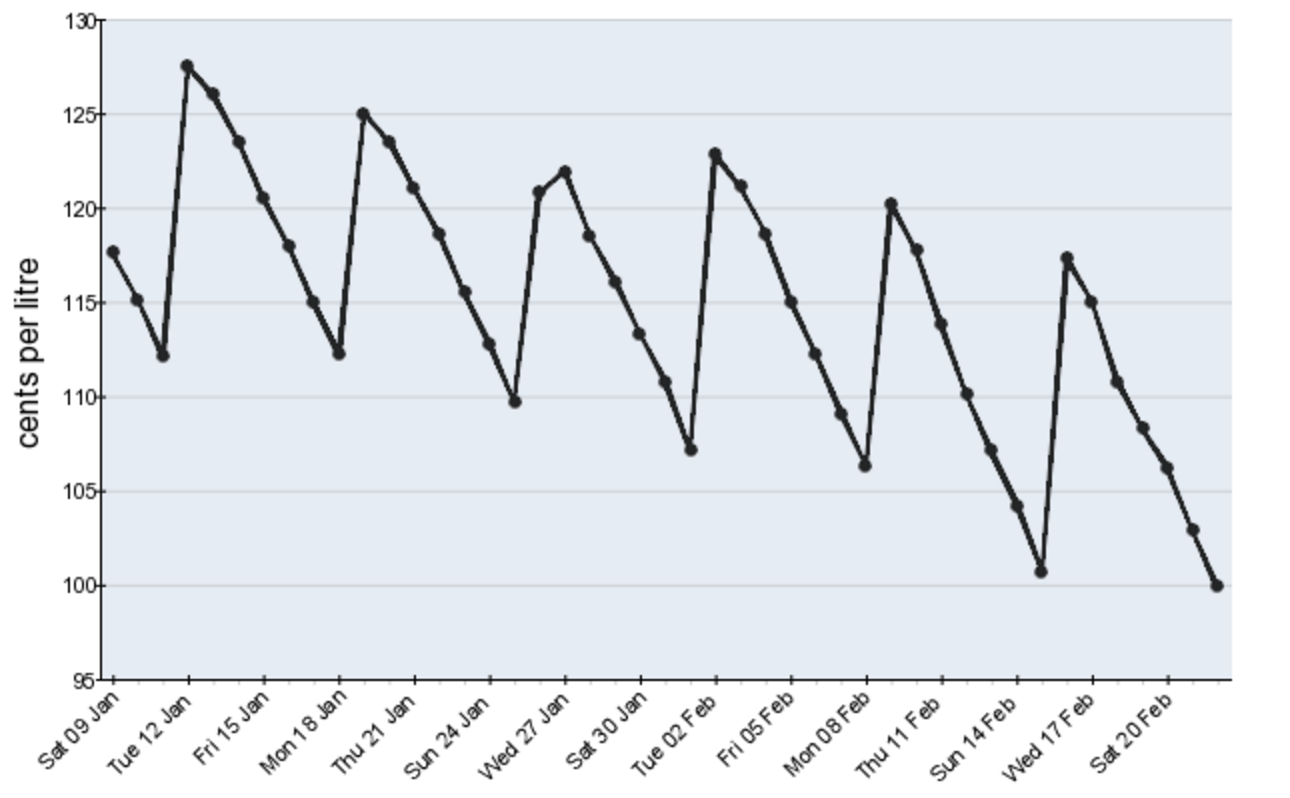
The overall trend of the data is a decreasing trend as we see the peak prices fall. This means petrol is getting cheaper to buy in Perth.
When we count the points in each cycle, we clearly see there are 7 points in each cycle. The easiest way to count these is from peak (highest point) to trough (lowest point) or vice versa. Thus a cycle lasts a week and there are seven "seasons" ,days or time periods per cycle.
There don't appear to be any start fluctuations or outliers, however it does appear that on Monday the 15th February 2016 the price dropped more steeply than usual. Monday seems to be the best time to buy petrol since this is when the price is at it's lowest in the cycle, and the price on this particular Monday was quite a bit lower than usual.
Example 2
The graph below shows house and apartment prices in Melbourne.
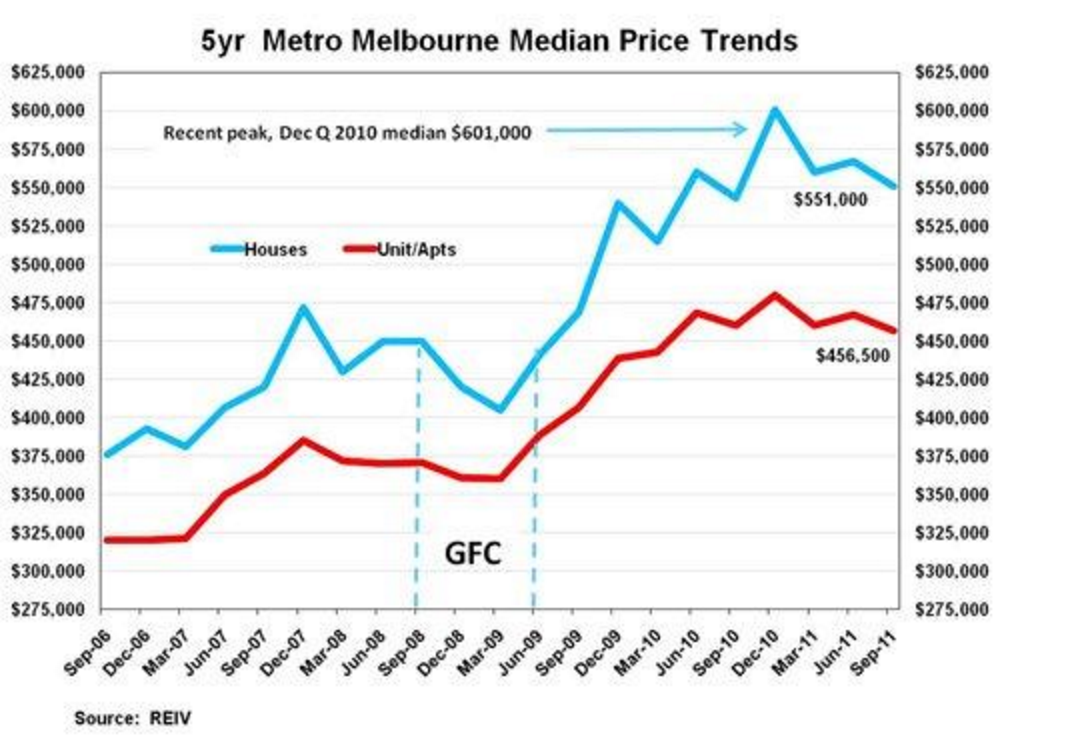
While we don't have enough detail to see the seasonality of the data, there's a lot of information we can see here.
We can see prices were flattening out leading up to the GFC - Global Financial Crisis, and then house prices took a bit of a dive. Recovery was fast and house prices rose rapidly with a big jump in December 2010. Almost a year later in September 2011, prices seem to be falling. At this time, investors would have been wondering whether they were in a pricing bubble (when the bubble bursts, prices drop rapidly) and there would be a lot of uncertainty in the market.
Worked Examples
Question 1:
Consider the following Time Series graph.
Describe the trend of the data:
Increasing
ADecreasing
BState the number of points per cycle:
There are $\editable{}$ points per cycle.
Question 2:
Consider the following set of Time Series data:
| Time Period | $1$1 | $2$2 | $3$3 | $4$4 | $5$5 | $6$6 | $7$7 | $8$8 | $9$9 | $10$10 | $11$11 | $12$12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data | $5$5 | $10$10 | $18$18 | $1$1 | $11$11 | $20$20 | $7$7 | $13$13 | $22$22 | $10$10 | $15$15 | $25$25 |
Plot this data on the graph below.
Loading Graph...Here is the graph with segments between each point:
Loading Graph...State the number of seasons (points per cycle) in this data.
There are $\editable{}$ seasons in each cycle of this data.
Describe the trend of the data:
Increasing
ADecreasing
BFor which time period is the recorded data most likely to indicate an outlier or unusual fluctuation?
Time Period = $\editable{}$