Trigonometry and Similarity
We we looked at similar triangles, we learnt that all the sides in similar triangles are in the same ratio. So, when we find the ratio of two sides in a triangle, the ratio of the corresponding sides in a similar triangle will always be the same.
As such, this means that the trigonometric ratios (sine, cosine and tangent) in similar right-angle triangles are always equal. Let's consider the two right-angled triangles below.
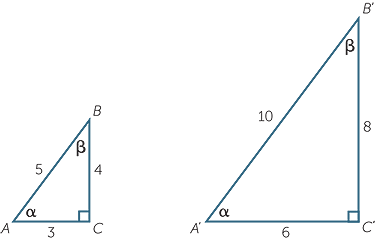
In triangle ABC:
| $\sin\alpha$sinα | $=$= | $\frac{4}{5}$45 | $\sin\beta$sinβ | $=$= | $\frac{3}{5}$35 | ||
| $\cos\alpha$cosα | $=$= | $\frac{3}{5}$35 | $\cos\beta$cosβ | $=$= | $\frac{4}{5}$45 | ||
| $\tan\alpha$tanα | $=$= | $\frac{4}{3}$43 | $\tan\beta$tanβ | $=$= | $\frac{3}{4}$34 |
In triangle A'B'C':
| $\sin\alpha$sinα | $=$= | $\frac{8}{10}$810 | $\sin\beta$sinβ | $=$= | $\frac{6}{10}$610 | ||
| $=$= | $\frac{4}{5}$45 | $=$= | $\frac{3}{5}$35 | ||||
| $\cos\alpha$cosα | $=$= | $\frac{6}{10}$610 | $\cos\beta$cosβ | $=$= | $\frac{8}{10}$810 | ||
| $=$= | $\frac{3}{5}$35 | $=$= | $\frac{4}{5}$45 | ||||
| $\tan\alpha$tanα | $=$= | $\frac{8}{6}$86 | $\tan\beta$tanβ | $=$= | $\frac{6}{8}$68 | ||
| $=$= | $\frac{4}{3}$43 | $=$= | $\frac{3}{4}$34 |
As you can see, the ratios are the same in both triangles.
So once we can prove that two triangles are similar, we can find corresponding trigonometric ratio, as well as corresponding angles and side lengths.
Examples
Question 1
Two right-angled triangles are measured, and a pair of corresponding angles are found to have a sine ratio of $\frac{240}{250}$240250 and $\frac{24}{25}$2425 respectively.
Are the two triangles similar?
Yes
ANo
B
Question 2
Consider the given triangles.

Are the two triangles similar?
Yes
ANo
BWhich rule confirms similarity?
Two pairs of angles are equal.
AThe ratio of three pairs of corresponding sides is equal.
BThe ratio of two pairs of corresponding sides is equal, and the pair of included angles are also equal.
C