Enlargements, Ratio and Scale Factors
Enlargements
A shape is considered an enlargement of another if one shape has side lengths that are all increased by the same scale factor.
For example:
Take a triangle with side lengths measuring $3$3cm, $4$4cm and $5$5cm. If each side is multiplied by the same factor, say $2$2, the new resulting triangle will have side lengths measuring $6$6cm, $8$8cm and $10$10cm. The resulting shape is larger.
Reductions
A shape is considered a reduction of another if one shape has side lengths that are all decreased by the same scale factor.
Consider the reverse of the above example: a triangle with side lengths measuring $6$6cm, $8$8cm and $10$10cm has each side multiplied by a factor of $\frac{1}{2}$12. The new resulting triangle will have side lengths measuring $3$3cm, $4$4cm and $5$5cm. The resulting shape is smaller than the original.
The scale factor tells us by how much the object has been enlarged or reduced.
The scale factor can be greater than $1$1: image is being made bigger than the original.
The scale factor can be smaller than $1$1: image is being made smaller than the original.
Example 1
The shape ABCD has been enlarged to A'B'C'D'.
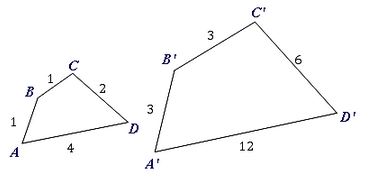
To find the scale factor we:
a) identify corresponding sides, in some cases this might mean rotating the shape.
b) look for a common multiple
By aligning the largest lengths sides with each other AD and A'D', and then the other sides I can set up this table.
| Side | Length | Side | Length | Scale factor |
|---|---|---|---|---|
| AD | $4$4 | A'D' | $12$12 | $12\div4=3$12÷4=3 |
| DC | $2$2 | D'C' | $6$6 | $6\div2=3$6÷2=3 |
| CB | $1$1 | C'B' | $3$3 | $3\div1=3$3÷1=3 |
| BA | $1$1 | B'A' | $3$3 | $3\div1=3$3÷1=3 |
Because shape A'B'C'D' has all side lengths $3$3 times larger than the corresponding sides of shape ABCD we say that it has been enlarged by a factor of $3$3.
Example 2
Is shape ABCD an enlargement of shape SPQR?
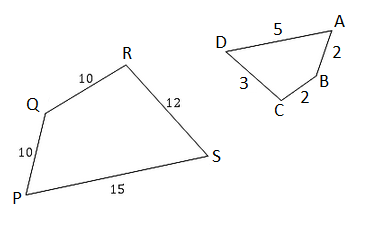
Firstly, we need to identify corresponding sides. To do this I will rotate SPQR.

Now I can see what might be the pairs of corresponding sides.
| SIDE | LENGTH | SIDE | LENGTH | SCALE FACTOR |
|---|---|---|---|---|
| AB | $2$2 | PQ | $10$10 | $10\div2=5$10÷2=5 |
| BC | $2$2 | QR | $10$10 | $10\div2=5$10÷2=5 |
| CD | $3$3 | RS | $12$12 | $12\div3=4$12÷3=4 |
| DA | $5$5 | SP | $15$15 | $15\div5=3$15÷5=3 |
As not all the sides have been decreased by the same scale, the shapes ABCD is not a reduction of PQRS.
example 3
Another place that enlargements are used is in scale drawings. Consider this image of a plan of a tower. If we know that the actual tower is $324$324m tall, and on this image the tower is $23.5$23.5cm we can actually deduce the scale factor.

| $\text{Scale factor }$Scale factor | $=$= | $\frac{\text{height of actual }}{\text{height of plan }}$height of actual height of plan |
| $=$= | $\frac{324m}{23.5cm}$324m23.5cm | |
| $=$= | $\frac{32400}{23.5}$3240023.5 cm | |
| $=$= | $1378.7234$1378.7234cm |
So the actual tower is $1378.72$1378.72 times the height of the image on the paper.
We would write this as a scale of $1$1cm$:$: $1378.72$1378.72cm
Worked Examples
Question 1
Which of these shapes are enlargements of each other?
 A
A B
B C
C D
D
Question 2
Triangle A'B'C' has been reduced to form a smaller triangle ABC. What is the scale factor?

$\frac{1}{4}$14
A$3$3
B$\frac{1}{3}$13
C$4$4
D
