Create and Interpret Scatter Plots
Correlations
A correlation is a way of expressing a relationship between two variables and, more specifically, how strongly pairs of data are related. We describe the correlation from data using language like positive correlation, negative correlation or no correlation. We can even further strengthen the language by using strong or weak.
Just because two variables correlate, even to a high degree, it does not imply that one causes the other. For example, there is a high degree of correlation between height and stride length. However, it doesn't mean that if you take big steps you'll grow taller!
Linear Patterns & Scatterplots
Linear patterns reveal whether or not two measurements are connected to each other. In other words, the presence of a linear pattern signals that the two sets of data correlate. One way of understanding these relationships is by plotting ordered pairs onto a scatterplot. This makes it easier to recognise patterns in the data, especially whether or not these patterns appear to be linear.
This linear relationship can be seen through close and consistent grouping in a scatterplot. The more closely the dots resemble a straight line, the stronger the correlation between the variables.
Positive Correlations
A positive correlation is when the data appears to gather in a positive relationship. Similar to a straight line with a positive gradient.
In other words, as one variable increases, the other variables also increases.
There are three types of positive correlation:
- Perfect positive correlation, where it lines up on a straight line exactly.
- Strong positive correlation, where it closely resembles a straight line with a positive gradient.
- Weak positive correlation, where the relationship is still positive.
For example, the scatterplot below shows a strong positive correlation between a person's height and arm span. You can see that as the first variable increases, the second increases too.
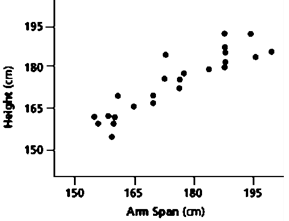
Linear Scatter
http://www.learner.org/courses/learningmath/data/session7/part_c/using.html
Here is a table of positive style correlations
 |
 |
 |
Negative Correlations
A negative correlation is when the data appears to gather in a negative relationship. Similar to a straight line with a negative gradient.
In other words, as one variable increases, the other one decreases.
Like positive correlation, there are three types of negative correlation:
- Perfect negative correlation, where it lines up on a decreasing line perfectly
- Strong negative correlation, where the data presents strongly in a negative direction
- Weak negative correlation.
The next scatterplot shows a strong negative correlation. You can see that as the first variable increases, the second variable decreases.
Here is a table of negative style correlations
 |
 |
 |
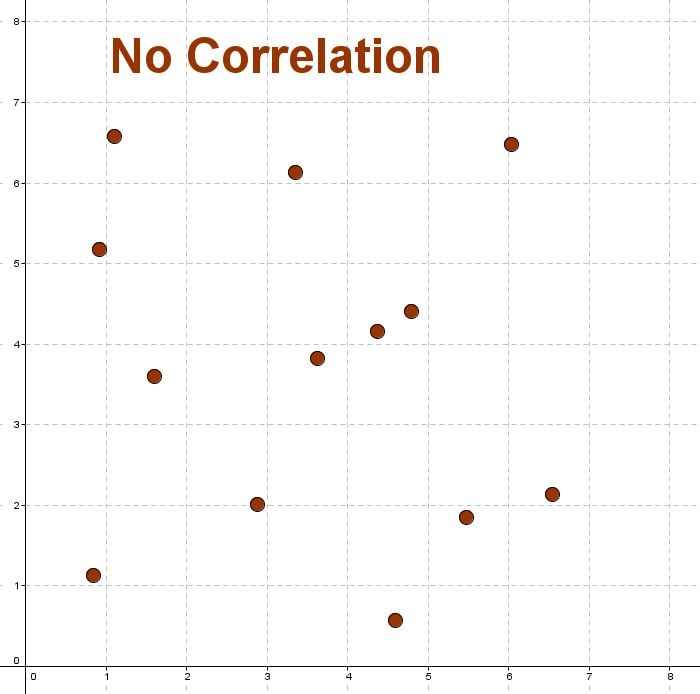
No Correlation
No correlation is when there is no relationship between the variables.
This means that there is a random or nonlinear relationship between the two sets of data.
Here is a diagram of no correlation
Examples
Question 1
Identify the type of correlation in the following scatter plot.

Think: If we drew a straight line through the points, what value would be close to the gradient?
Do: The correlation has a gradient close to $1$1, so this is a strong positive correlation.
Question 2
Consider the two variables: eye colour and IQ. Do you think there is a relationship between them?
Think: Do you think a person's eye colour has anything to do with their IQ?
Do: No there is no relationship between them?
Question 3
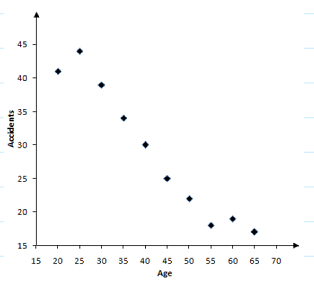
The following table shows the number of traffic accidents associated with a sample of drivers of different age groups.
| Age | Accidents |
|---|---|
| $20$20 | $41$41 |
| $25$25 | $44$44 |
| $30$30 | $39$39 |
| $35$35 | $34$34 |
| $40$40 | $30$30 |
| $45$45 | $25$25 |
| $50$50 | $22$22 |
| $55$55 | $18$18 |
| $60$60 | $19$19 |
| $65$65 | $17$17 |
Which of the following scatter plots correctly represents the above data?
 A
A B
B C
CIs the correlation between a person's age and the number of accidents they are involved in positive or negative?
Positive
ANegative
BIs the correlation between a person's age and the number of accidents they are involved in strong or weak?
Strong
AWeak
BWhich age group's data represent an outlier?
30-year-olds
ANone of them
B65-year-olds
C20-year-olds
D
Question 4
Consider the table of values that show four excerpts from a database comparing the income per capita of a country and the child mortality rate of the country. If a scatter plot was created from the entire database, what relationship would you expect it to have?
| Income per capita | Child Mortality rate |
|---|---|
| $1465$1465 | $67$67 |
| $11428$11428 | $16$16 |
| $2621$2621 | $35$35 |
| $32468$32468 | $9$9 |
Strongly positive
ANo relationship
BStrongly negative
C
EXTENSION
Further Information - Correlation Coefficient
As we have seen, a correlation is a way of expressing a relationship between two variables and, more specifically, how strongly pairs of data are related. We can measure this mathematically by looking at the correlation coefficient ($r$r). The correlation coefficient is a number between $-1$−1 and $+1$+1. It is similar to the gradient of a straight line and once the correlation coefficient is calculated, we can more accurately determine whether there is positive correlation, negative correlation or no correlation.
Positive Correlations
There are three types of positive correlation:
- Perfect positive correlation, where $r$r is $+1$+1 exactly
- Strong positive correlation, where $r$r is close to $+1$+1
- Weak positive correlation, where $r$r still greater than $0$0 but not as close to $+1$+1
Negative Correlations
Like positive correlation, there are three types of negative correlation:
- Perfect negative correlation, where $r$r is $-1$−1 exactly
- Strong negative correlation, where $r$r is close to $-1$−1
- Weak negative correlation, where $r$r is still less than $0$0 but not as close to $-1$−1
No Correlation
No correlation is when $r$r is close or equal to $0$0.
In other words, there is no relationship between the variables.
This means that there is a random or nonlinear relationship between the two sets of data.
If there are no linear relationships between two sets of data then the scatterplot shows a more random distribution. In other words, when there is no correlation (ie. $r=0$r=0), the dots in a scatterplot will be all over the place.
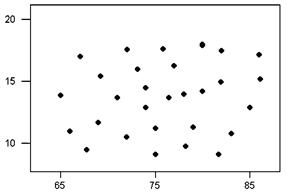
Random Scatter
http://wps.prenhall.com/esm_walpole_probstats_7/55/14203/3635978.cw/content/index.html