8.03 Line segments and constructions
Introduction
Points, lines, and planes form the foundation of Geometry. Although lines are infinite, line segments can be constructed, measured, compared, and labeled using various postulates and terms.
Postulates that help us find the lengths of various line segments are introduced in this lesson. We will learn how to draw basic geometric constructions, from copying a line to bisecting a line, using a pencil and paper with a compass and using technology.
Line segments
There are two postulates in Geometry that allow us to measure and solve problems involving segment lengths.
A segment can be bisected, which means it has been divided into two congruent segments. The midpoint, which bisects a segment, is the point exactly halfway between the two endpoints of a segment.
Examples
Example 1
Use the ruler postulate to find the length of \overline{XZ}.
Example 2
Use the segment addition postulate to find the length of the following:
QS
PQ
Example 3
Point B bisects \overline{AC}.
Identify two congruent segments.
If AB=7, find the length of \overline{AC}.
Line segments can be measured using the ruler postulate by aligning the segment with a number line and finding the difference between the values each point lines up with. We can solve problems involving line segments using the segment addition postulate. Congruent segments can be labeled with congruency marks. Midpoints and bisectors are two ways a segment can be divided into congruent segments.
Geometric constructions
A geometric construction is the accurate drawing of angles, lines, and shapes. The tools used for these constructions are a straightedge, compass, and pencil.
To construct a copy of a segment, we will:
- Identify the segment we want to copy.
- Draw a point that will become the first endpoint of the copied segment.
- Open the compass width to measure the distance between endpoints.
- Without changing the compass width, place the point end of the compass on the point we constructed for the copy and draw a small arc. Place a point anywhere on the arc.
- Connect the two points using a straightedge.
To construct the bisector of a segment, we will:
- Identify the segment we want to bisect.
- Open the compass width to just past half the segment's length and draw an arc from one endpoint that extends to both sides of the segment.
- Without changing the compass width, draw another arc from the other endpoint that intersects the original arc on both sides of the segment.
- Label the intersection of the arcs with points.
- Connect the points.
Examples
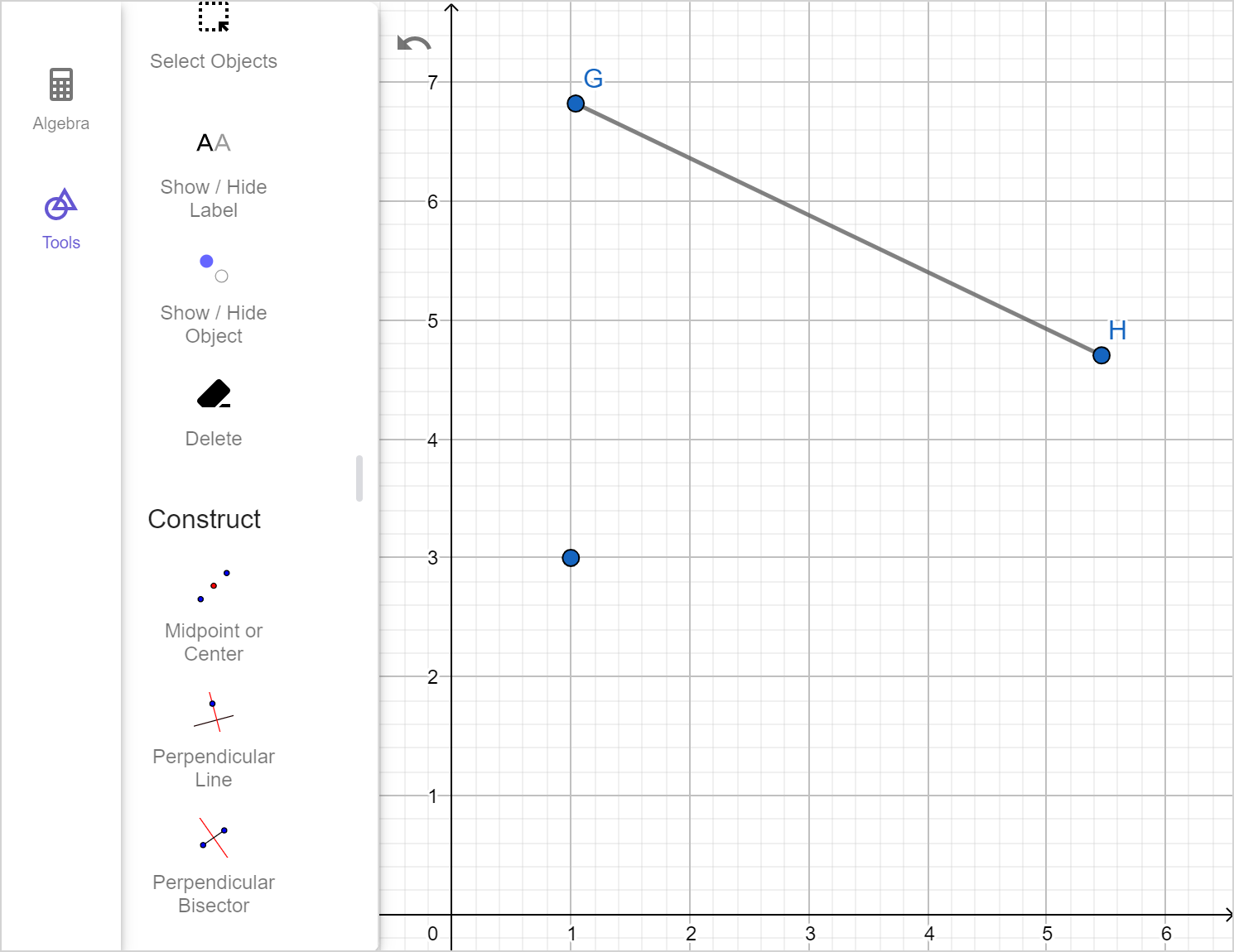
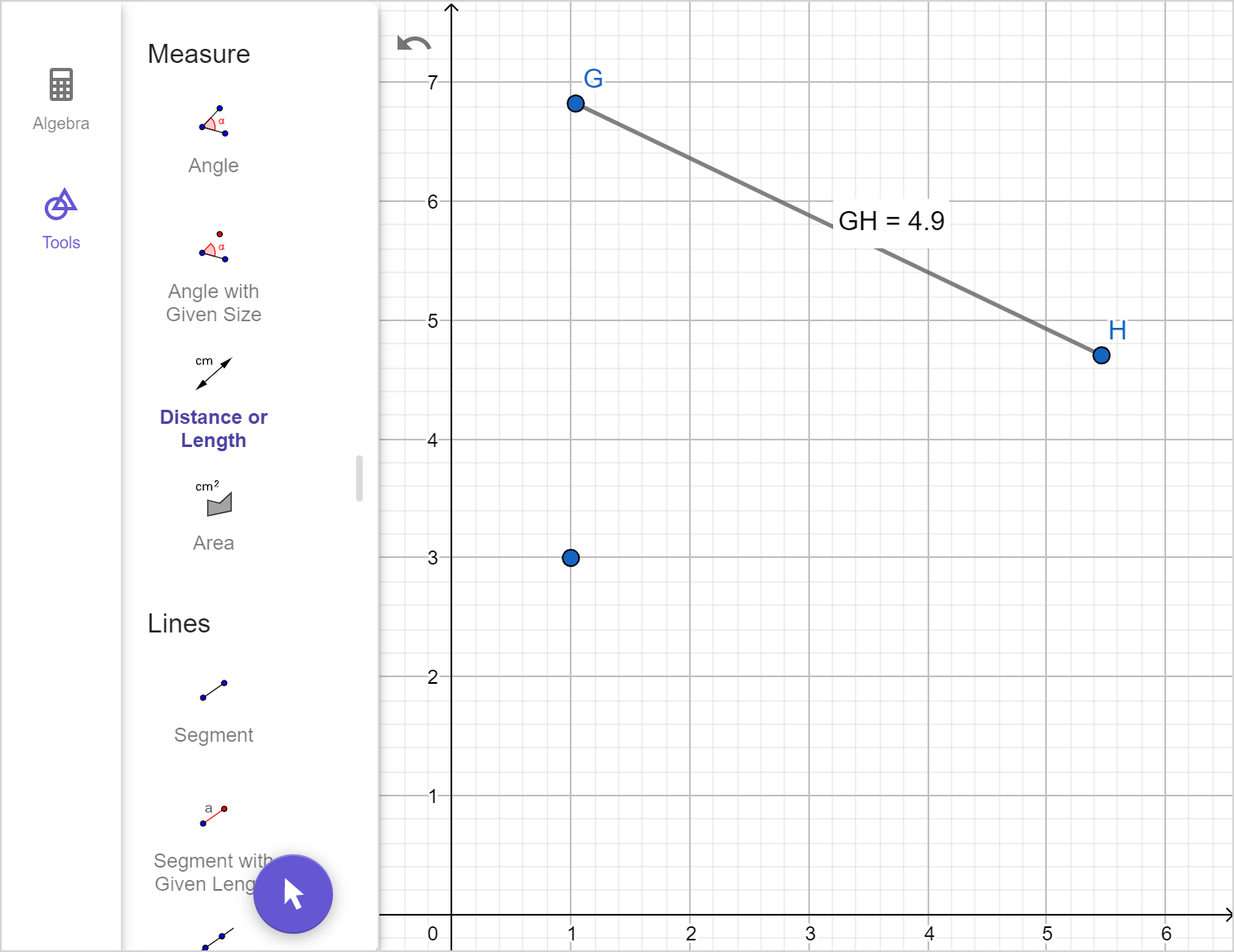
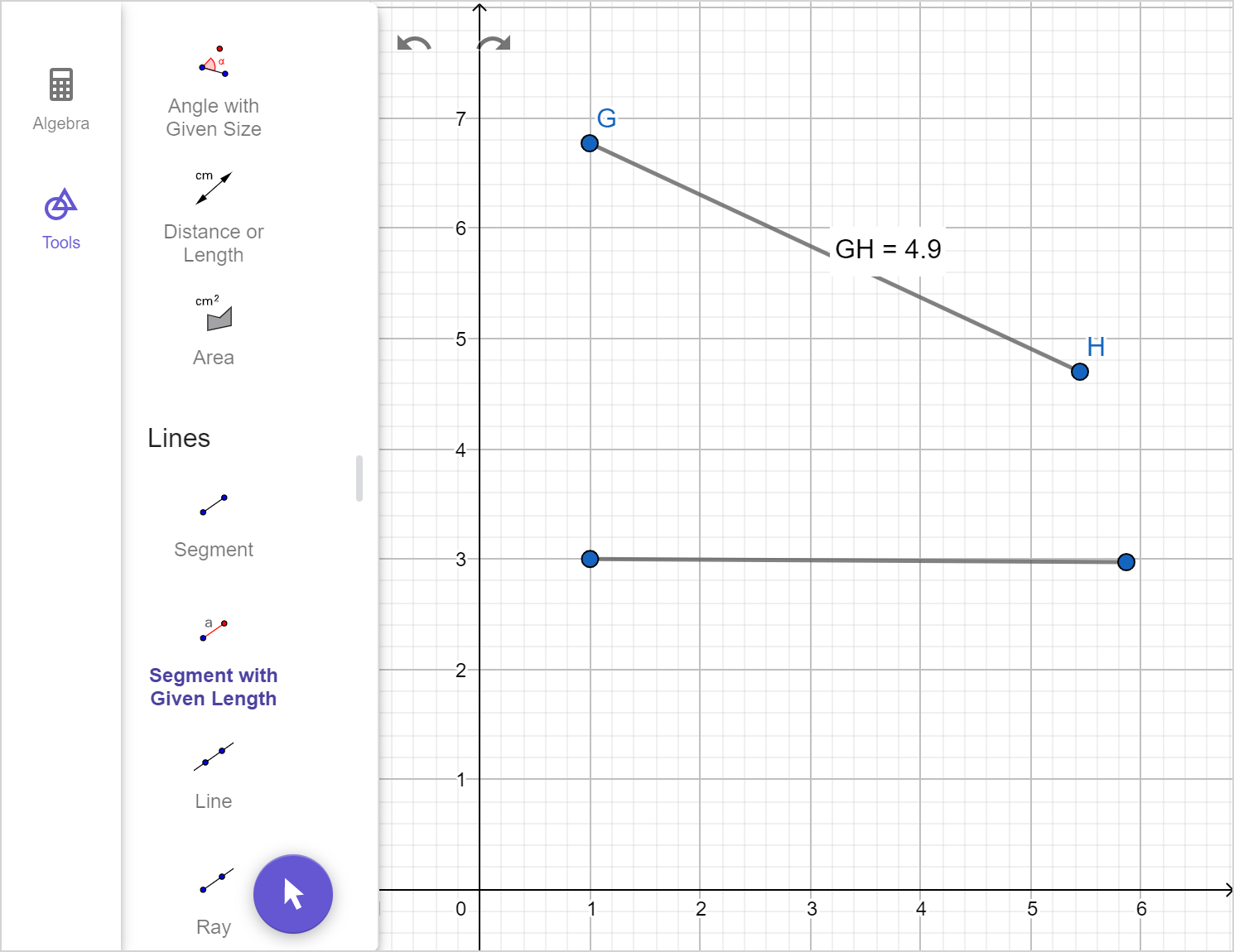
Example 4
Construct a copy of \overline{GH}.
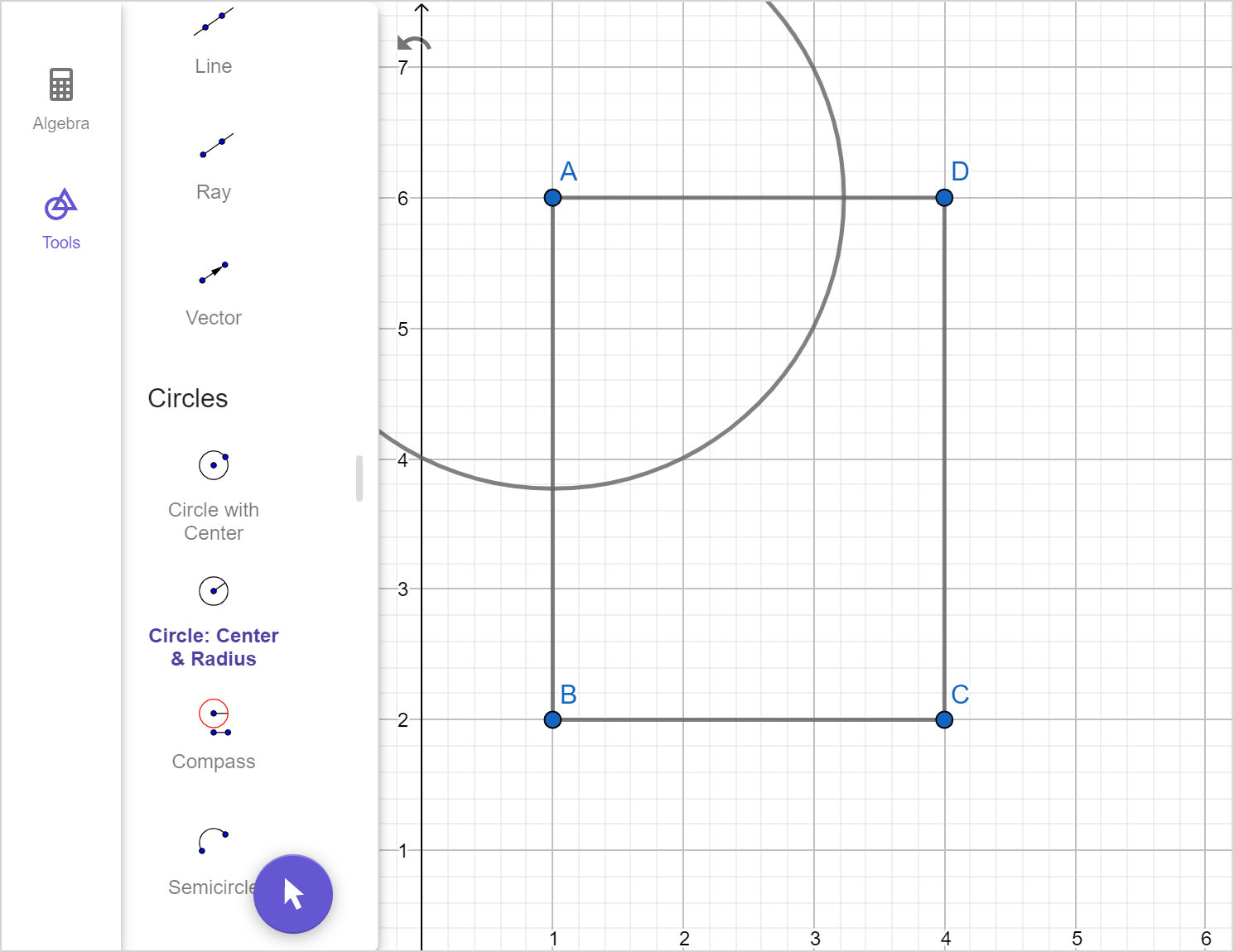
Example 5
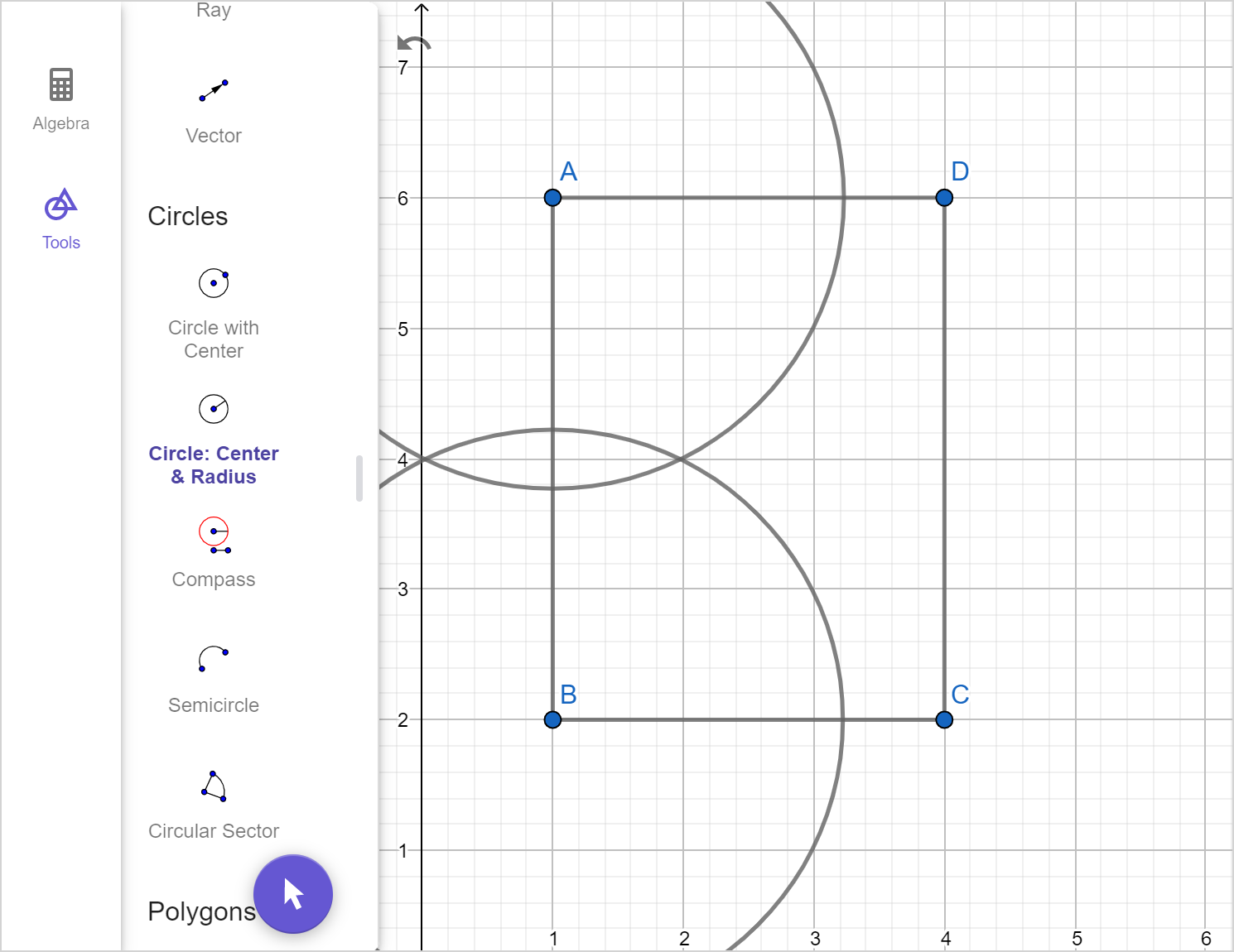
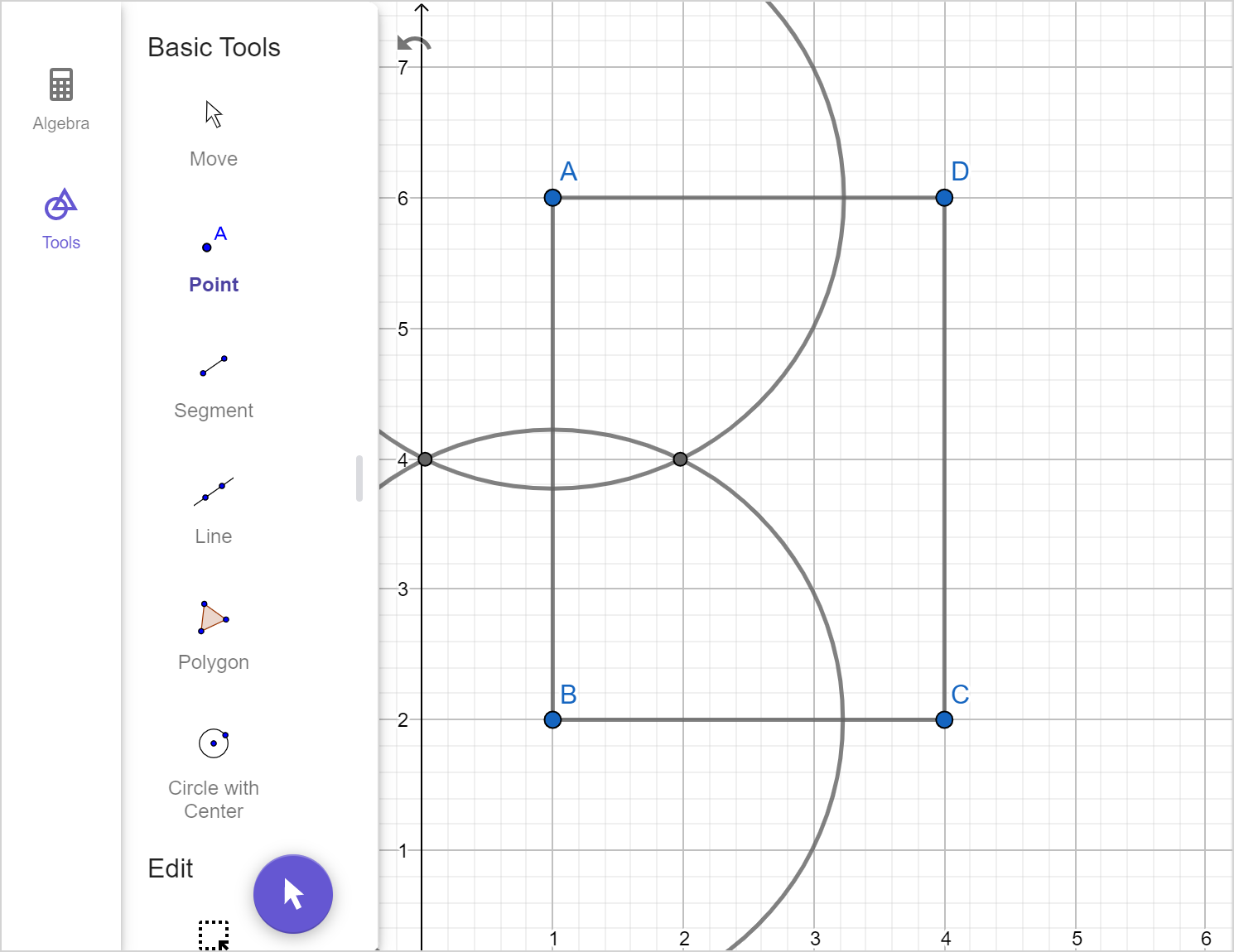
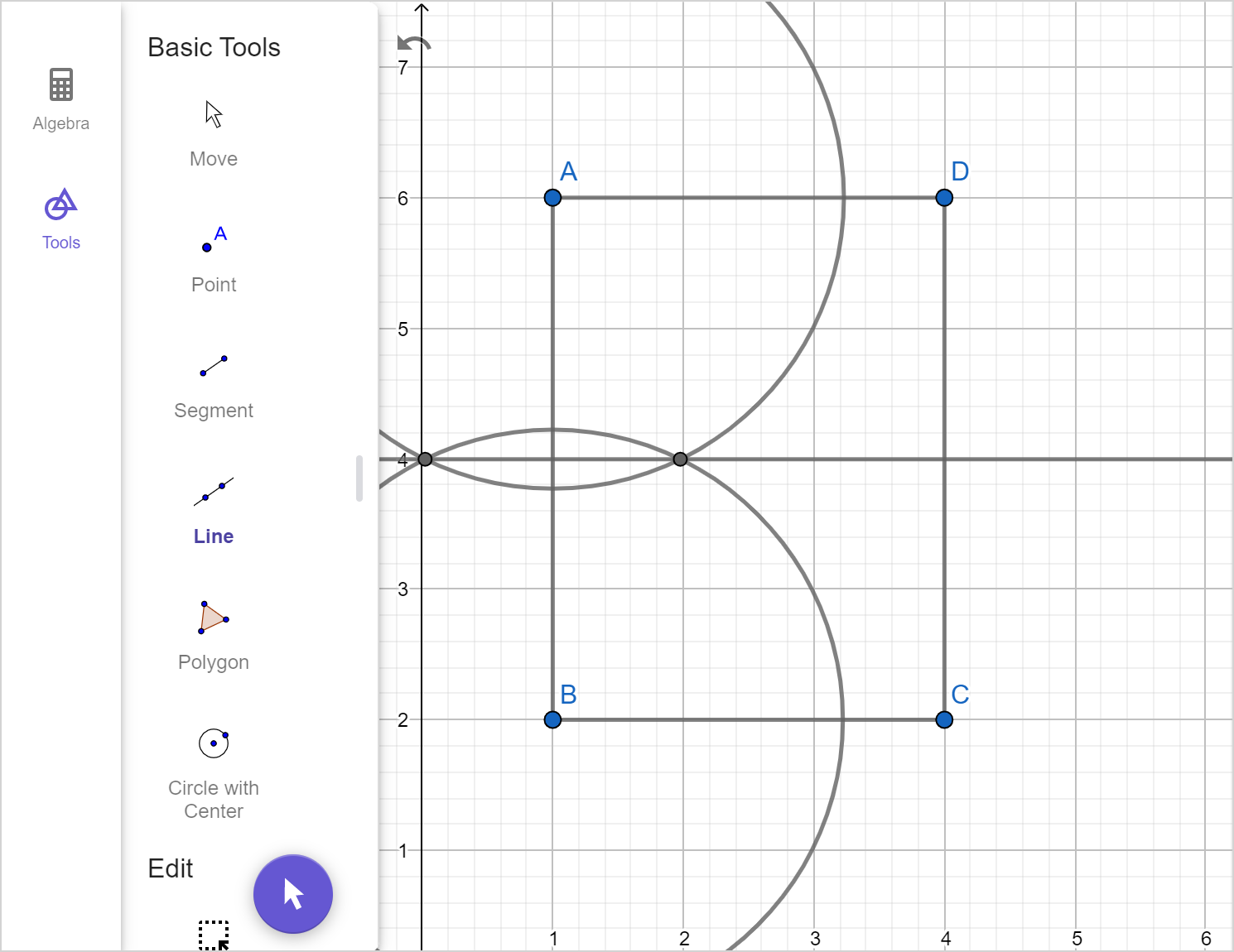
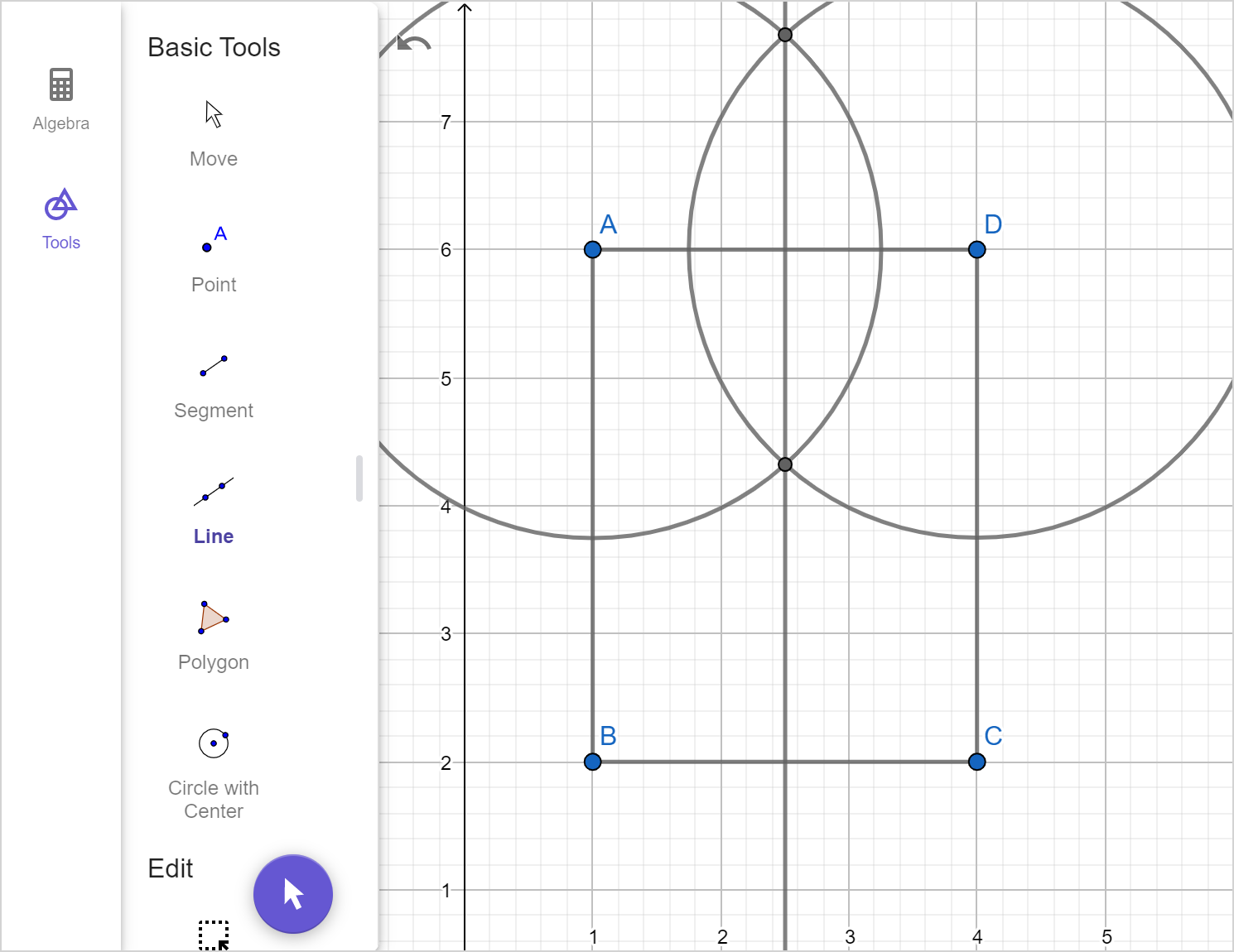
Ursula has a rectangular fenced sheep enclosure, shown below. She wants to build an additional fence that will divide the enclosure into two congruent rectangular sections.
Construct a line to represent the additional fence, showing all steps.
Geometric figures can be constructed using a compass and straight edge. We can copy a line segment to any point using congruent circles and bisect a line segment using overlapping congruent circles.