Topics
7. Inverse Functions and Logarithms
topic badge
United States of America
Grades 9-12

7.01 Inverse functions

Lesson
Practice

Introduction

We sketched the inverse graphs of linear functions and algebraically found inverses in Algebra 1 lesson  3.07 Inverses of linear functions  . This lesson applies the same concepts to radical, rational, and polynomial functions. In some cases, we will need to restrict the domain in order to create inverse functions.

Inverse relations

Inverse operations are operations that 'undo' each other - for example, addition and subtraction, or multiplication and division. We can extend this concept to find the inverse of an entire function.

Inverse relation

A relation that reverses the original relation. The graph of an inverse relation is the original graph reflected across the line y=x.

Inverses are useful for determining the input of a relation if the outputs are known. Consider a situation where a plane is traveling at a constant speed, and we want to know how long the plane has been flying over certain distances. Rather than using the function d\left(t\right)=rt and dividing by the rate to find the time for each of the distances, we can simply rewrite the equation as t=\dfrac{d}{r}. This is the inverse relation of d\left(t\right).

We can find the algebraic equation for the inverse relation by completing the following steps:

  1. Write f\left(x\right) as y

  2. Swap x and y

  3. Solve for y

Swapping the x and y variables in a relationship will exchange the coordinates for any point on the graph. Thus, the domain and range will be switched in an inverse relation compared to the original relation.

Geometrically, this means that the relation and its inverse are mirror images of each other across the line y=x.

Examples

Example 1

The volume of a sphere is modeled by the equation V\left(r\right)=\dfrac{4}{3}\pi r^3.

a

For each of the following volumes, find the radius of the corresponding sphere.

  • 288\pi
  • \frac{243\pi}{2}
  • \frac{4000}{81}\pi
Worked Solution
Create a strategy

To find the radius for each of the spheres, we can substitute the given volumes into the equation and solve for r.

Apply the idea

  • For the sphere with a volume of 288\pi:

    \displaystyle 288\pi\displaystyle =\displaystyle \frac{4}{3}\pi r^3Substitute V\left(r\right)=288\pi
    \displaystyle 216\pi\displaystyle =\displaystyle \pi r^3Multiply both sides by \dfrac{4}{3}
    \displaystyle 216\displaystyle =\displaystyle r^3Divide both sides by \pi
    \displaystyle 6\displaystyle =\displaystyle rCube root both sides

  • For the sphere with a volume of \dfrac{243\pi}{2}:

    \displaystyle \frac{243\pi}{2}\displaystyle =\displaystyle \frac{4}{3}\pi r^3Substitute V\left(r\right)=\dfrac{243\pi}{2}
    \displaystyle \frac{729\pi}{8}\displaystyle =\displaystyle \pi r^3Multiply both sides by \dfrac{4}{3}
    \displaystyle \frac{729}{8}\displaystyle =\displaystyle r^3Divide both sides by \pi
    \displaystyle \frac{9}{2}\displaystyle =\displaystyle rCube root both sides

  • For the sphere with a volume of \dfrac{4000}{81}\pi:

    \displaystyle \frac{4000}{81}\pi\displaystyle =\displaystyle \frac{4}{3}\pi r^3Substitute V\left(r\right)=\dfrac{4000}{81}\pi
    \displaystyle \frac{1000}{27}\pi\displaystyle =\displaystyle \pi r^3Multiply both sides by \dfrac{4}{3}
    \displaystyle \frac{1000}{27}\displaystyle =\displaystyle r^3Divide both sides by \pi
    \displaystyle \frac{10}{3}\displaystyle =\displaystyle rCube root both sides
Reflect and check

Notice that the input for the volume function is the radius. In each of these problems, we were given the output and needed to solve for the input.

b

Describe a more efficient way to find the radius when the volume is known.

Worked Solution
Create a strategy

In the previous part, we repeated the same steps each time to solve for the radius. Rather than repeating the steps, we need to find a way to reduce the overall number of steps.

Apply the idea

Rather than substituting the volume and solving for the radius each time, it would be more efficient to solve for the radius initially. This allows us to use the steps of solving for the radius only once, rather than repeating the same steps three times.

\displaystyle V\displaystyle =\displaystyle \frac{4}{3}\pi r^3Function for volume of a sphere
\displaystyle \frac{3}{4}V\displaystyle =\displaystyle \pi r^3Multiply both sides by \dfrac{4}{3}
\displaystyle \frac{3V}{4\pi}\displaystyle =\displaystyle r^3Divide both sides by \pi
\displaystyle \sqrt[3]{\frac{3V}{4\pi}}\displaystyle =\displaystyle rCube root both sides

Now that we have solved for the radius, we simply need to substitute and evaluate.

\displaystyle r\displaystyle =\displaystyle \sqrt[3]{\frac{3\left(288\pi\right)}{4\pi}}Substitute V=288\pi
\displaystyle =\displaystyle 6
\displaystyle r\displaystyle =\displaystyle \sqrt[3]{\frac{3\left(\frac{243\pi}{2}\right)}{4\pi}}Substitute V=\frac{243\pi}{2}
\displaystyle =\displaystyle \frac{9}{2}
\displaystyle r\displaystyle =\displaystyle \sqrt[3]{\frac{3\left(\frac{4000}{81}\pi\right)}{4\pi}}Substitute V=\frac{4000}{81}\pi
\displaystyle =\displaystyle \frac{10}{3}

Overall, this method requires fewer steps.

c

Explain how your answer to part (b) relates to the equation for volume.

Worked Solution
Create a strategy

In part (b), we said it was more efficient to solve for the radius first, then substitute the volume and evaluate. This question asks us to describe the relationship between r=\sqrt[3]{\dfrac{3V}{4\pi}} and V=\dfrac{4}{3}\pi r^3. We can do this by considering the independent and dependent variables in each equation.

Apply the idea

V\left(r\right) is a function of the radius. This means the volume changes based on the radius. When we solve the volume equation for r, we are rewriting it to represent the radius as a function of the volume. In other words, the independent and dependent variables have switched in each equation.

  • V=\dfrac{4}{3}\pi r^3
    • Independent variable: r
    • Dependent variable: V
  • r=\sqrt[3]{\dfrac{3V}{4\pi}}
    • Independent variable: V
    • Dependent variable: r

Therefore, r=\sqrt[3]{\dfrac{3V}{4\pi}} and V=\dfrac{4}{3}\pi r^3 are inverses of each other.

Reflect and check

Normally when solving for the inverse relation, we swap the independent and dependent variables first. If we did that for this problem, we would get V=\sqrt[3]{\dfrac{3r}{4\pi}} as the equation for the inverse. However, this does not make sense contextually because the inverse solves for the radius, not the volume.

The reason we switch the variables when finding the inverse is to allow for a way to graph both relations. To do this, we need the independent variable (the variable of the horizontal axis) and the dependent variable (the variable on the vertical axis) to be the same for both equations.

Since x is generally used for the independent variable and y is generally used for the dependent variable, writing both equations as "y in terms of x" makes it easier for us to understand and graph the equations.

\displaystyle y\displaystyle =\displaystyle \dfrac{4}{3}\pi x^3Original relation
\displaystyle y\displaystyle =\displaystyle \sqrt[3]{\dfrac{3x}{4\pi}}Inverse relation
-4
-3
-2
-1
1
2
3
4
x
-4
-3
-2
-1
1
2
3
4
y

Example 2

Complete the tables. State which relations are inverses.

x-2-1012
f\left(x\right)=2x^3
x-2-1012
g\left(x\right)=\frac{1}{2}x^3
x-16-20216
h\left(x\right)=\sqrt[3]{\frac{x}{2}}
x-1-\frac{1}{8}0\frac{1}{8}1
j\left(x\right)=2\sqrt[3]{x}
Worked Solution
Create a strategy

To complete each of the tables, we will substitute each value of x into the given function. To determine which relations are inverses, we need to examine the inputs and outputs. The inputs and outputs of inverse relations will be swapped.

Apply the idea
x-2-1012
f\left(x\right)=2x^3-16-20216
x-2-1012
g\left(x\right)=\frac{1}{2}x^3-4-\frac{1}{2}0\frac{1}{2}4
x-16-20216
h\left(x\right)=\sqrt[3]{\frac{x}{2}}-2-1012
x-1-\frac{1}{8}0\frac{1}{8}1
j\left(x\right)=2\sqrt[3]{x}-2-1012

Looking at the tables, we can see that the inputs of f\left(x\right) are the outputs of h\left(x\right), and the outputs of f\left(x\right) are the inputs of h\left(x\right). Therefore, f\left(x\right) and h\left(x\right) are inverse relations. These are the only two functions where the outputs and inputs are swapped, so these are the only inverse relations.

Reflect and check

Using technology to graph both functions on the same coordinate plane, we can see that these functions are reflections of each other across the line y=x.

-3
-2
-1
1
2
3
x
-3
-2
-1
1
2
3
y

Example 3

Consider the absolute value function y=\left|x+3\right|+6.

State the domain and range of the inverse relation.

Worked Solution
Create a strategy

Since the inverse relation is defined by switching the independent and dependent variables, the domain of the function is the range of the inverse, and the range of the function is the domain of the inverse.

We can use transformations to graph the original function and determine its domain and range.

Apply the idea

The original function is in the form y=\left|x-h\right|+k where h represents a horizontal translation and k represents a vertical translation. In this function, h=-3 and k=6. This means the function has been translated left 3 units and up 6 units.

-10
-8
-6
-4
-2
2
x
2
4
6
8
10
12
y

Analyzing the graph, we can see that the domain is \left(-\infty,\infty\right) and the range is \left[6,\infty\right).

Therefore, the domain of the inverse relation is \left[6,\infty\right) and the range is \left(-\infty,\infty\right).

Reflect and check

We can check our answer by identifying points on the graph of the function, swapping the x- and y-values, and using them to graph the inverse relation.

-8
-6
-4
-2
2
4
6
8
10
x
-8
-6
-4
-2
2
4
6
8
10
y

This verifies that the domain of the inverse relation is \left[6,\infty\right) and the range is \left(-\infty,\infty\right).

Idea summary

We can verify a relation's inverse by graphing the relations to show the two relations are reflected across the line y=x.

We can find the inverse by:

  • Algebraically swapping x and y and solving the equation for y
  • Graphically swapping the x and y coordinates

Inverse functions

Exploration

Explore the applet by choosing a function and dragging the slider to produce the function's inverse.

Loading interactive...
  1. The inverse of a linear function is also always a function. What do you notice about the inverse of each of these parent functions?
  2. How does restricting the domain make a relation become a function?

Any function can be reflected across the line y=x to create an inverse relation, but not all inverse relations will satisfy the definition of a function.

Inverse function

Two functions f and g are said to be inverses when one function can be mapped to the other by a reflection across the line y=x. That is, for every point \left(x,y\right) in f, there is a point \left(y,x\right) in g.

The function inverse to f\left(x\right) is denoted f^{-1}\left(x\right).

All inverse functions are inverse relations, much like all functions are relations, but not all inverse relations are inverse functions.

Functions whose inverse is also a function are called one-to-one functions and have special properties.

One-to-one function

A function that returns a unique element in the range for each element in their domain

Note that in order to be a function, a relation maps each input to exactly one output. A one-to-one function includes the additional criteria that the function must map each output to exactly one input.

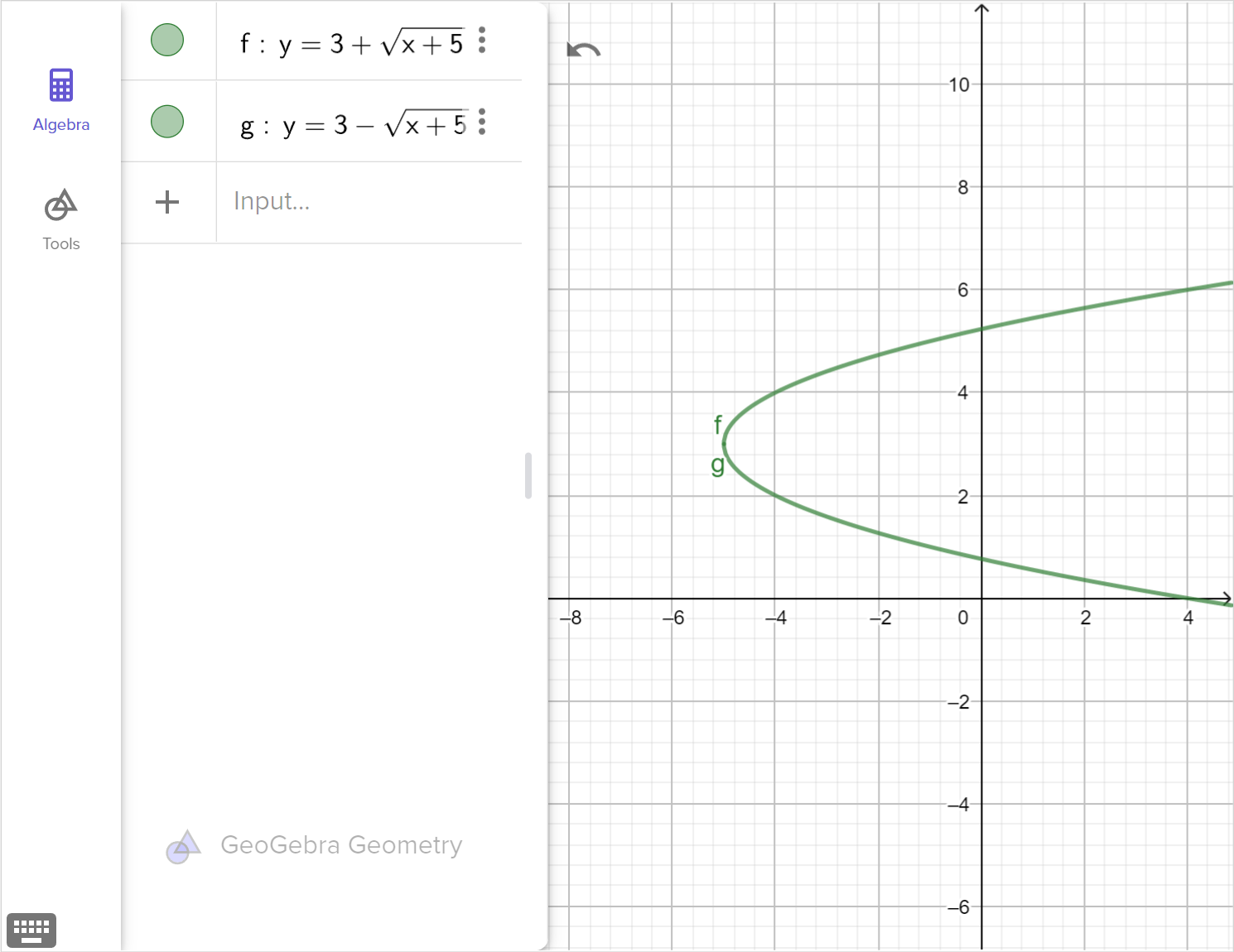
For example, let's consider f \left(x \right)=x^2. The inverse relation is x=y^2 or y=\pm \sqrt{x}. For any input value, x \geq 0, there will be two output values: one positive and one negative. Therefore, this inverse relation is not a function.

-8
-6
-4
-2
2
4
6
8
x
-8
-6
-4
-2
2
4
6
8
y

We can also see this graphically. When we reflect y = x^2 across y=x, we can see that the inverse relation does not pass the vertical line test - a vertical line drawn through the graph has more than one point of intersection.

We do not have to actually reflect a function across y=x in order to graphically determine whether or not a function's inverse is a function. Instead, we can visually check whether or not a function is one-to-one by using a horizontal line test.

If a horizontal line can be drawn through all range values of the original function without intersecting the graph at more than one point, then each output value will only map to one input value, and the function is a one-to-one function and its inverse will also be a function.

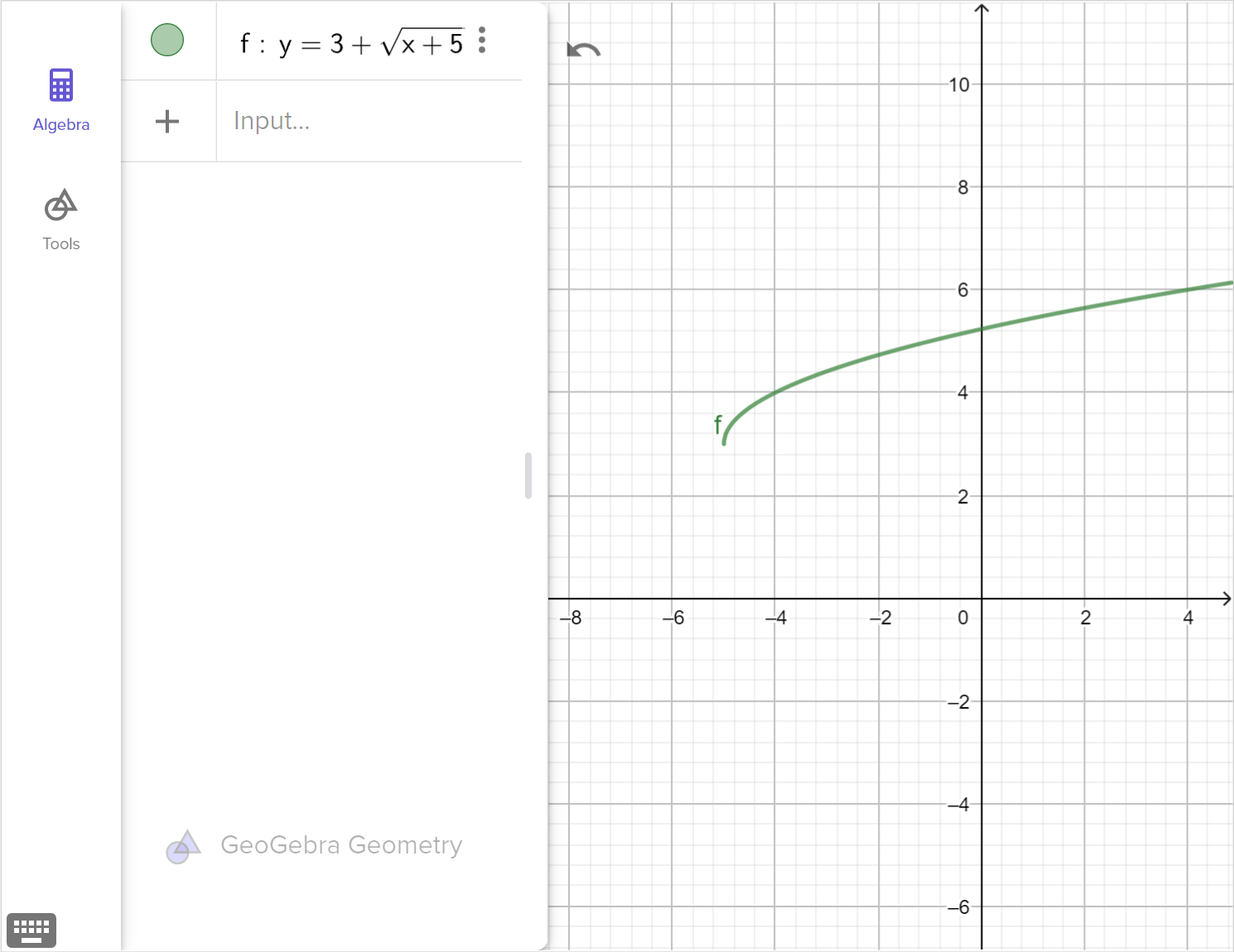
If we restrict the domain of y=x^2 to x\geq0, it will now pass the horizontal line test and have an inverse function, namely y=\sqrt{x}.

-8
-6
-4
-2
2
4
6
8
x
-8
-6
-4
-2
2
4
6
8
y

Examples

Example 4

Consider the graphs of f\left(x\right), g\left(x\right) and h\left(x\right) and determine if they have an inverse function without any domain restrictions. Explain how you know.

-8
-6
-4
-2
2
4
6
8
x
-8
-6
-4
-2
2
4
6
8
y
a

f\left(x\right)

Worked Solution
Apply the idea

f\left(x\right) appears to be a linear function with a negative slope.

-8
-6
-4
-2
2
4
6
8
x
-8
-6
-4
-2
2
4
6
8
y
  • We can graph the inverse relation by reflecting f\left(x\right) across the line y=x
-8
-6
-4
-2
2
4
6
8
x
-8
-6
-4
-2
2
4
6
8
y
  • We can then determine if the inverse relation is a function by drawing a vertical line through the function, and determining the number of times they intersect
  • We can see that there is only one point of intersection

All of this confirms that the original function f\left(x\right) was one-to-one.

We can see that f\left(x\right) has an inverse function since it is a one-to-one function.

Reflect and check

As the two functions are reflections of each other across the line y=x, we could instead apply the horizontal line test on f\left(x\right).

-8
-6
-4
-2
2
4
6
8
x
-8
-6
-4
-2
2
4
6
8
y
  • If it only intersects in one place then there will be an inverse function, without any domain restrictions.
  • If it has more than one point of intersection there is not an inverse function
  • We can see that there is only one point of intersection.

The horizontal line test also tells us that f\left(x\right) is a one-to-one function. Since f\left(x\right) is a function and the horizontal line test tells us each point in the output is unique. Asking if a function "has an inverse function without any domain restrictions" is equivalent to asking if a function is one-to-one.

b

g\left(x\right)

Worked Solution
Apply the idea

g\left(x\right) appears to be a quadratic function opening upwards.

-8
-6
-4
-2
2
4
6
8
x
-8
-6
-4
-2
2
4
6
8
y
  • We can graph the inverse relation by reflecting f\left(x\right) across the line y=x
  • We can then determine if the inverse relation is a function by drawing a vertical line through the function, and determining the number of times they intersect
  • We can see that there are two points of intersection

All of this confirms that the original function g\left(x\right) was not a one-to-one function.

We can see that g\left(x\right) does not have an inverse function.

Reflect and check

Alternatively, we could perform the horizontal line test on g\left(x\right), revealing the function is not a one-to-one function.

-8
-6
-4
-2
2
4
6
8
x
-8
-6
-4
-2
2
4
6
8
y

However, if g\left(x\right) had a restricted domain of either \left[0, \infty\right) or \left( -\infty, 0\right], then it would have an inverse function, as we can see below for \left[0, \infty\right).

-8
-6
-4
-2
2
4
6
8
x
-8
-6
-4
-2
2
4
6
8
y
c

h\left(x\right)

Worked Solution
Apply the idea

h\left(x\right) appears to be a non-linear function with a negative slope.

-8
-6
-4
-2
2
4
6
8
x
-8
-6
-4
-2
2
4
6
8
y
  • We can graph the inverse relation by reflecting h\left(x\right) across the line y=x
-8
-6
-4
-2
2
4
6
8
x
-8
-6
-4
-2
2
4
6
8
y
  • We can then determine if the inverse relation is a function by drawing a vertical line through the function, and determining the number of times they intersect
  • We can see that there is only one point of intersection

All of this confirms that the original function h\left(x\right) was one-to-one.

We can see that h\left(x\right) has an inverse function because it is a one-to-one function.

Reflect and check

As the two functions are reflections of each other across the line y=x, we could instead apply the horizontal line test on h\left(x\right).

-8
-6
-4
-2
2
4
6
8
x
-8
-6
-4
-2
2
4
6
8
y
  • If it only intersects in one place then there will be an inverse function, without any domain restrictions
  • If it has more than one point of intersection there is not an inverse function
  • We can see that there is only one point of intersection

The horizontal line test also tells us that h\left(x\right) is a one-to-one function. Since h\left(x\right) is a function and the horizontal line test tell us each point in the output is unique.

Example 5

For each of the following functions:

  • Determine an expression for the inverse relation.
  • State whether or not the inverse is a function.
  • If the inverse is not a function, find a restricted domain for the function under which the inverse is a function.
a

y = \left(x-3\right)^2-5

Worked Solution
Create a strategy

We want to swap x and y, and then solve for y. We can then check whether the inverse is a function using the vertical line test.

Apply the idea

Inverse:

\displaystyle x\displaystyle =\displaystyle \left(y-3\right)^2-5 Swap x and y
\displaystyle x+5\displaystyle =\displaystyle \left(y-3\right)^2Add 5 to both sides
\displaystyle \pm\sqrt{x+5}\displaystyle =\displaystyle y-3Evaluate the square root of both sides
\displaystyle 3\pm\sqrt{x+5}\displaystyle =\displaystyle yAdd 3 to both sides

y=3\pm\sqrt{x+5} is the inverse of y=\left(x-3\right)^2-5.

We now need to determine if y=3\pm\sqrt{x+5} is a function. Graphing y=3\pm\sqrt{x+5} using technology, it is clear to see that it does not pass the vertical line test and therefore is not a function.

A screenshot of the GeoGebra geometry tool showing the graphs of y equals 3 plus square root of x plus 5 and y equals 3 minus square root of x plus 5. Speak to your teacher for more details.

We can restrict the domain of y= \left(x - 3 \right) ^2 - 5 to x \geq 3, and it will have the inverse function y= 3 + \sqrt{x+5}.

A screenshot of the GeoGebra geometry tool showing the graph of y equals 3 plus square root of x plus 5. Speak to your teacher for more details.
Reflect and check

As the graph of a quadratic function does not pass the horizontal line test, no quadratic functions have inverses without domain restrictions.

Alternatively, we could have restricted the domain to x\leq 3 in which case the inverse would have been y=3-\sqrt{x+5}.

-5
-4
-3
-2
-1
1
2
3
4
5
x
-5
-4
-3
-2
-1
1
2
3
4
5
y
b

y=\left(x- 4 \right) \left(x^2 +4x + 16 \right)

Worked Solution
Create a strategy

Inverse:

Swap x and y, and then solve for y. We can determine whether the inverse is a function by using the vertical line test.

Apply the idea
\displaystyle x\displaystyle =\displaystyle \left(y- 4 \right) \left(y^2 +4y + 16 \right)Swap x and y
\displaystyle x\displaystyle =\displaystyle y^3+4y^2+16y -4y^2 -16y -64Multiply the polynomials
\displaystyle x\displaystyle =\displaystyle y^3-64Combine like terms
\displaystyle x+64\displaystyle =\displaystyle y^3Add 64 to both sides
\displaystyle \sqrt[3]{x+64}\displaystyle =\displaystyle yEvaluate the cube root of both sides

y=\sqrt[3]{x+64} is the inverse of y=\left(x- 4 \right) \left(x^2 +4x + 16 \right).

We now need to determine if y=\sqrt[3]{x+64} is a function. Graphing y=\sqrt[3]{x+64} using technology, the relation passes the vertical line test and therefore is a function.

A screenshot of the GeoGebra geometry tool showing the graphs of y equals cube root of x plus 64. Speak to your teacher for more details.
c

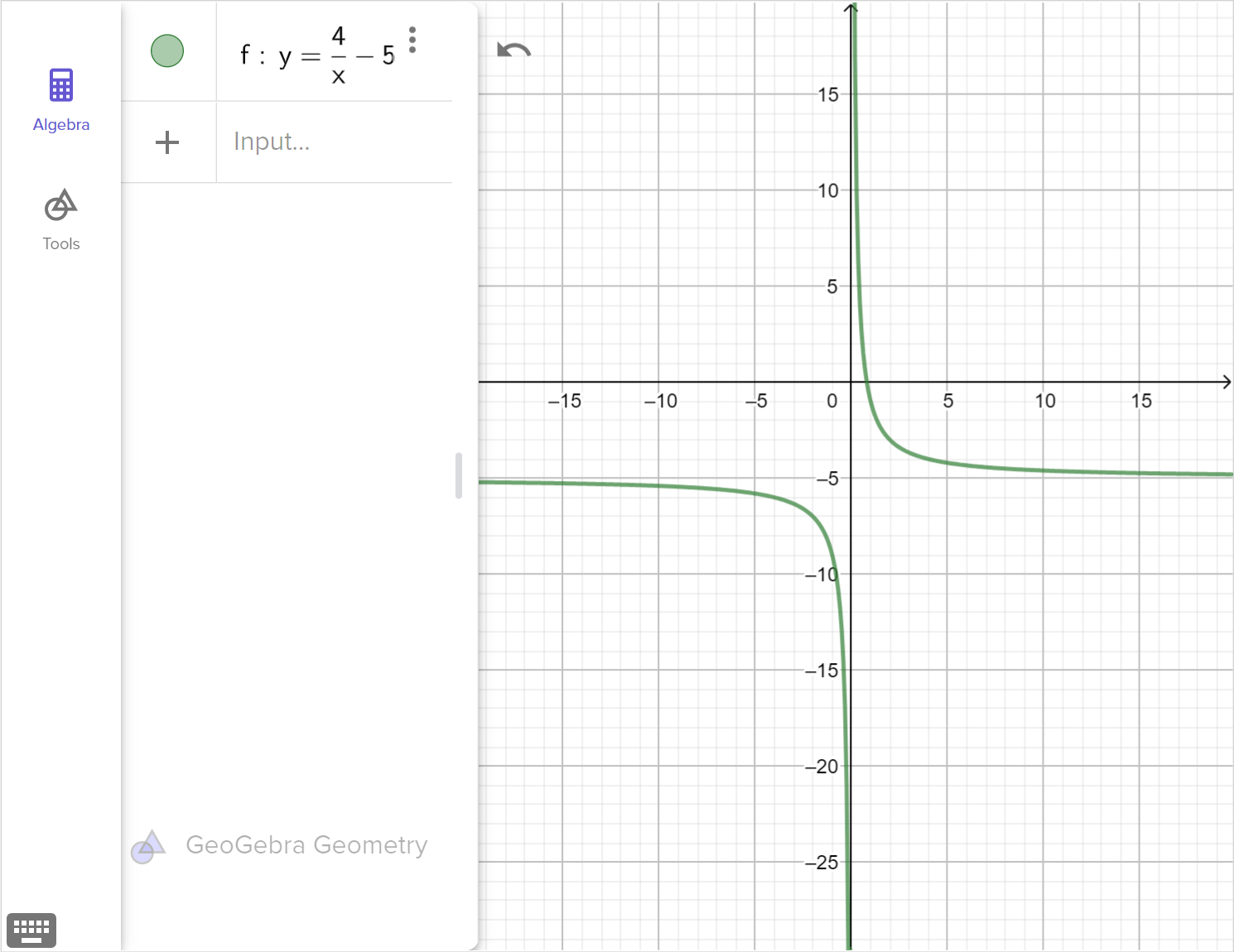
f \left(x \right) = \dfrac{4}{x+5}

Worked Solution
Create a strategy

Since this is written as a function, we will begin by writing f\left(x\right) as y. Then, we can swap x and y, solve for y, and determine whether the inverse is a function by using the vertical line test.

Apply the idea
\displaystyle y\displaystyle =\displaystyle \dfrac{4}{x+5}Write f\left(x\right) as y

Inverse:

\displaystyle x\displaystyle =\displaystyle \dfrac{4}{y+5}Swap x and y
\displaystyle x\left(y+5\right)\displaystyle =\displaystyle 4Multiply both sides by y+5
\displaystyle y+5\displaystyle =\displaystyle \frac{4}{x}Divide both sides by x
\displaystyle y\displaystyle =\displaystyle \frac{4}{x}-5Subtract 5 from both sides

y=\dfrac{4}{x}-5 is the inverse of y=\dfrac{4}{x+5}.

We now need to determine if y=\dfrac{4}{x}-5 is a function. Graphing y=\dfrac{4}{x}-5 using technology, we see the relation passes the vertical line test. Although it appears the graph may fail the vertical line test near the y-axis, we know that this is a rational function and that there is a vertical asymptote at x=0 since this value makes the denominator undefined. Therefore, y=\dfrac{4}{x}-5 is a function.

A screenshot of the GeoGebra geometry tool showing the graph of y equals 4 over x minus 5. Speak to your teacher for more details.
Reflect and check

Alternatively, after multiplying both sides by y+5 when finding the inverse, we could have distributed x to find a different form of the inverse function.

\displaystyle x\left(y+5\right)\displaystyle =\displaystyle 4Multiply both sides by y+5
\displaystyle xy+5x\displaystyle =\displaystyle 4Distribute x
\displaystyle xy\displaystyle =\displaystyle 4-5xSubtract 5x from both sides
\displaystyle y\displaystyle =\displaystyle \frac{4-5x}{x}Divide both sides by x

We can subtract the terms of y=\dfrac{4}{x}-5 to see that it is equivalent to y=\dfrac{4-5x}{x}, so they are the same function in different forms. If we didn't use technology to graph the inverse, it would be better to use the form y=\dfrac{4}{x}-5 so we can identify and use the transformations to graph it.

Example 6

Consider the function shown in the table below.

x123456
f\left(x\right)32168421
a

Determine if it is possible for an inverse function to exist without restricting the domain.

Worked Solution
Create a strategy

For an inverse function to exist without restricting the domain, we need to determine whether there is only one output for every input. In other words, no outputs can be repeated.

Apply the idea

Looking at the table, we see that each input and each output is unique. Therefore, an inverse function does exist without needing to restrict the domain.

Reflect and check

If we plot these points, we would see that the function would pass the horizontal line test which means it is one-to-one.

1
2
3
4
5
6
7
x
5
10
15
20
25
30
35
y
b

Determine the value of f^{-1}\left(8\right).

Worked Solution
Create a strategy

The domain of the inverse function is the range of the original function. Since we know that 8 is in the domain of the inverse, we need to find which x-value of the original function produces an output of 8.

We can also view this in terms of function mapping. Each point \left(x,y\right) in the original function can be mapped to a point \left(y,x\right) in the inverse function.

Apply the idea

In the original function, the point \left(3,8\right) is mapped to the point \left(8,3\right) in the inverse function.

Therefore, f^{-1}\left(8\right)=3.

c

Determine the value of x that makes f^{-1}\left(x\right)=1.

Worked Solution
Create a strategy

The range of the inverse function is the domain of the original function. Since we know that 1 is in the range of the inverse, we need to find which output of the original function is produced by an input of 1.

Apply the idea

In the original function, the point \left(1,32\right) is mapped to the point \left(32,1\right) in the inverse function.

Therefore, f^{-1}\left(32\right)=1.

Idea summary

We can determine if a function's inverse is also a function by using the horizontal line test on the function. If the inverse is not a function, we can restrict the domain of the given function.

Outcomes

F.BF.B.4

Find inverse functions.

F.BF.B.4.A

Solve an equation of the form f(x) = c for a simple function f that has an inverse and write an expression for the inverse.

F.BF.B.4.C (+)

Read values of an inverse function from a graph or a table, given that the function has an inverse.

F.BF.B.4.D (+)

Produce an invertible function from a non-invertible function by restricting the domain.

What is Mathspace

About Mathspace