Topics
7. Inverse Functions and Logarithms
topic badge
United States of America
Grades 9-12

7.03 Solving radical equations

Lesson
Practice

Introduction

We learned about the inverse of a power function in lessons  7.01 Inverse functions  and lesson  7.02 Graphing radical functions  . We will solve equations of radical functions by applying the inverse operation, taking a power. The restricted domain of even root functions will potentially impact the types of solutions resulting from solving radical equations.

Solving radical equations

The process of solving radical equations is similar to solving a linear equation, that is, by using inverse operations. The inverse of a square root operation is squaring, and the inverse of an nth root, is to take the nth power.

Radical equations

An equation containing at least one radical expression

x
y

Recall that the parent function f\left(x\right)=\sqrt{x} has a domain of x\geq0, and a range of y\geq0.

When we are solving equations involving square roots, and other even roots, we need to remember that on every step of our solution, any radicands must be non-negative and any radicals must also be non-negative.

The solution to the equation, however, can be negative.

When solving questions with real life applications, we also need to ensure we have viable solutions, which make sense within the context of the question. A non-viable solution does not make sense within the context of the question, such as a negative value when we are solving for the length of a physical object.

Exploration

Asha solves the following radical equation and states the solutions are x=-2 and x=-9:\sqrt{x+18} = x+6

Shown below is the graph of the system of equations represented by the radical equation: y = \begin{cases} \sqrt{x+18} \\ x+6 \end{cases}

The graphs of y equals square root of x plus 18 and y equals x plus 6 plotted in the four quadrant coordinate plane.
  1. Algebraically check the given solutions to the equation \sqrt{x+18}= x+6.
  2. Based on the graph, what is the solution the to the system of equations formed by the equation \sqrt{x+18} = x+6?
  3. How do you think Asha obtained an additional solution?

When solving radical equations, it is possible to have an extraneous solution. This is why checking solutions to radical equations is an important part of solving radical equations.

Extraneous solution

A solution to an equation that emerges from the algebraic process of solving the problem, but is not a valid solution

Examples

Example 1

Solve the following equations:

a

\sqrt{y}+5=9

Worked Solution
Create a strategy

To solve for y, we first want to isolate \sqrt{y}, we can then square both sides of the equation.

Apply the idea
\displaystyle \sqrt{y}+5 \displaystyle =\displaystyle 9State the equation
\displaystyle \sqrt{y} \displaystyle =\displaystyle 4Subtraction property of equality
\displaystyle \left(\sqrt{y}\right)^2\displaystyle =\displaystyle 4^2Square both sides
\displaystyle y\displaystyle =\displaystyle 16Evaluate the squares
Reflect and check

We can see that if we substitute y=16 into the original equation we obtain \sqrt{16}+5=9 which is a true statement, and as \sqrt{16} is positive we have a valid solution.

b

\sqrt[3]{4x-9}=-1

Worked Solution
Create a strategy

To solve for x, we first want to isolate 4x-9 by raising each side of the equation to a power of 3. We are then left with a linear equation we can solve using more inverse operations

Apply the idea
\displaystyle \sqrt[3]{4x-9} \displaystyle =\displaystyle -1State the equation
\displaystyle \left(\sqrt[3]{4x-9}\right)^3 \displaystyle =\displaystyle \left(-1\right)^3Raise both sides to a power of 3
\displaystyle 4x-9\displaystyle =\displaystyle -1Evaluate the cubes
\displaystyle 4x\displaystyle =\displaystyle 8Addition property of equality
\displaystyle x\displaystyle =\displaystyle 2Division property of equality
Reflect and check

We can see that if we substitute x=2 into the original equation we obtain \sqrt[3]{-1}=-1 which is a true statement. When dealing with odd valued indexes such as \sqrt[3]{x}, we do not need to worry about the radicand being negative.

Raising both sides of an equation to an odd power is reversible. If a=b then a^3=b^3 and if a^3=b^3 then a=b.

Example 2

For each of the following equations:

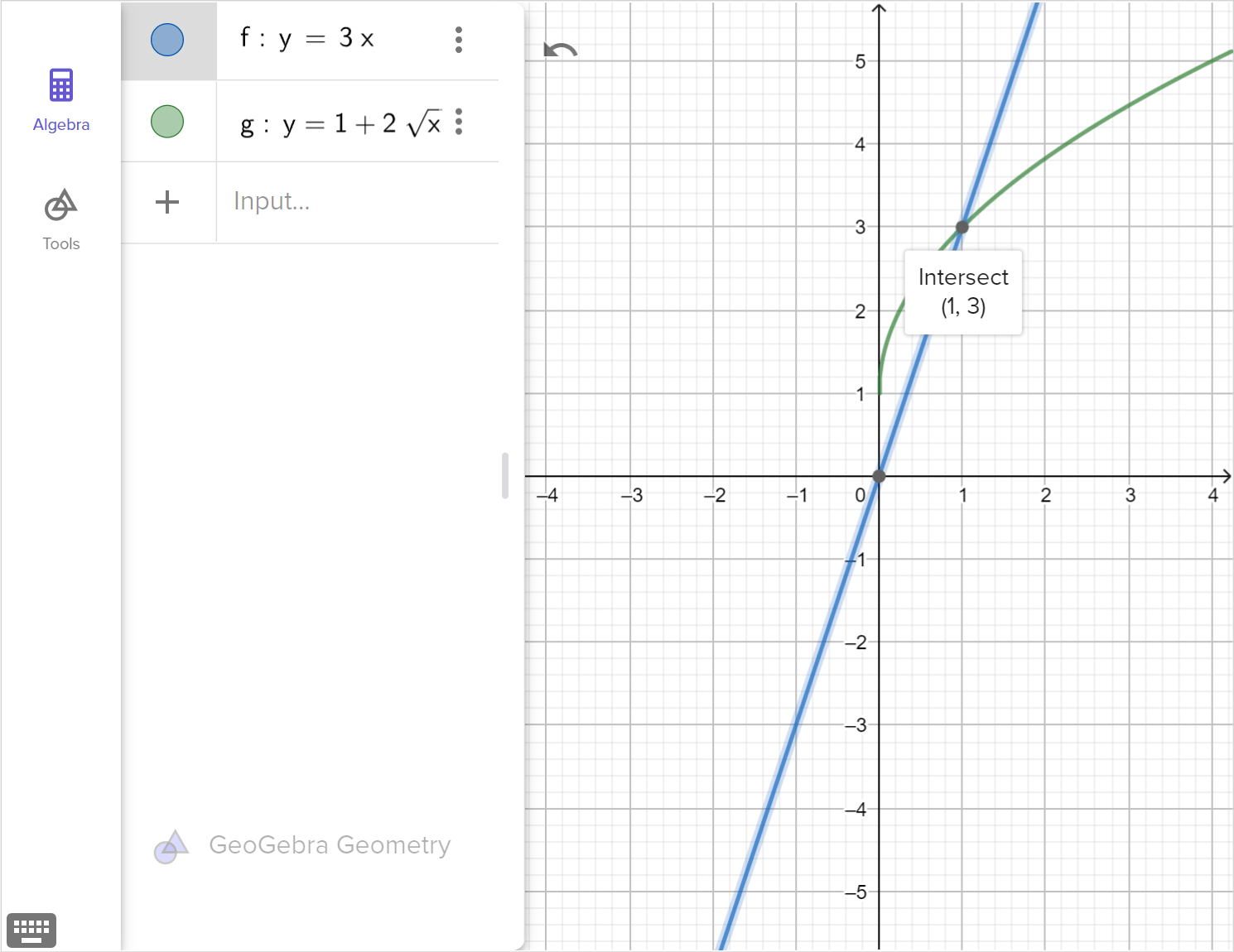
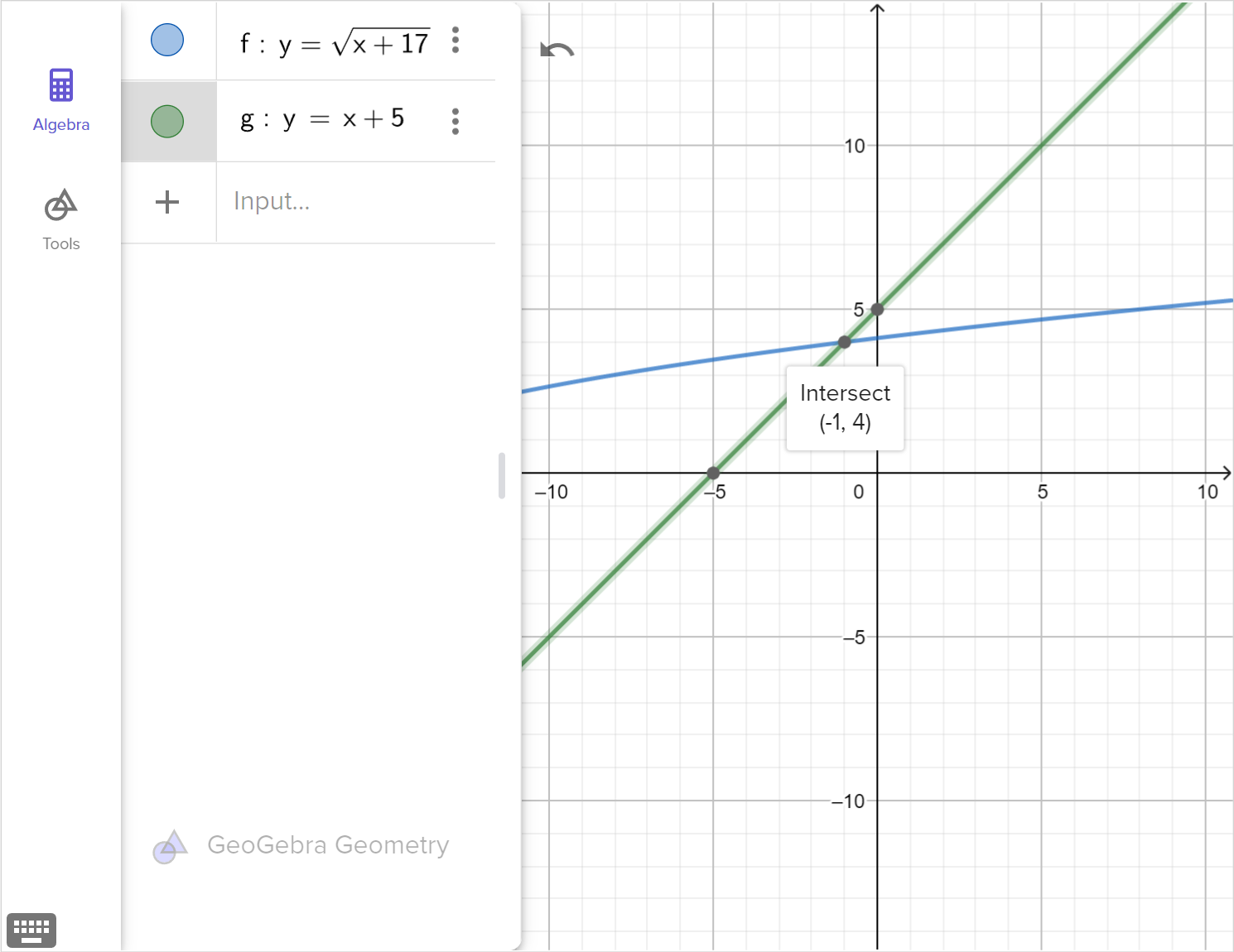
  1. Solve each equation for x and identify any extraneous solutions
  2. Write the equation as a system of equations
  3. Graph each system of equations
a

3x=1+2\sqrt{x}

Worked Solution
Create a strategy

To solve for x, we first want to isolate 2\sqrt{x}. We can then square both sides of the equation to remove the radical. We can then solve the resulting quadratic equation. We then want to check for extraneous solutions.

Apply the idea
  1. \displaystyle 3x\displaystyle =\displaystyle 1+2\sqrt{x}State the equation
    \displaystyle 3x-1\displaystyle =\displaystyle 2\sqrt{x}Subtract 1 from both sides
    \displaystyle \left(3x-1\right)^2\displaystyle =\displaystyle \left(2\sqrt{x}\right)^2Square both sides
    \displaystyle 9x^2-6x+1\displaystyle =\displaystyle 4xEvaluate the exponents
    \displaystyle 9x^2-10x+1\displaystyle =\displaystyle 0Subtract 4x from both sides
    \displaystyle \left(9x-1\right)\left(x-1\right)\displaystyle =\displaystyle 0Factor the quadratic

    Using the zero product rule we get two solutions x=\dfrac{1}{9}, x=1. We now want to test both solutions:

    \displaystyle 3\left(1\right)\displaystyle =\displaystyle 1+2\sqrt{1}Substitute x=1
    \displaystyle 3\displaystyle =\displaystyle 3Evaluate the multiplication and addition

    We can see that x=1 satisfies the original equation and is a valid solution.

    Now, let's test x=\dfrac{1}{9}.

    \displaystyle 3\left(\dfrac{1}{9}\right)\displaystyle =\displaystyle 1+2\sqrt{\frac{1}{9}}Substitute x=\dfrac{1}{9}
    \displaystyle \frac{1}{3}\displaystyle =\displaystyle \frac{5}{3}Evaluate the multiplication and addition

    We can see that x=\dfrac{1}{9} leads to a false statement and is therefore an extraneous solution.

  2. The equation 3x=1+2\sqrt{x} can be written as the system of equations: \begin{cases} y= 3x \\ y= 1 + 2 \sqrt{x} \end{cases}

  3. We can use technology to graph the system of equations.

    A screenshot of the GeoGebra geometry tool showing the graphs of y equals 3 x and y equals 1 plus 2 square root of x. The point of intersection of the graphs is highlighted. Speak to your teacher for more details.
Reflect and check

We can see the solution x=1 as the point of intersection on the graph, while the extraneous solution found algebraically, x=\dfrac{1}{9}, does not appear on the graph.

b

\sqrt{x+17}=x+5

Worked Solution
Create a strategy

To solve for x, we first want to square both sides of the equation to remove the radical. We can then solve the resulting quadratic equation. We then want to check for extraneous solutions.

Apply the idea
  1. \displaystyle \sqrt{x+17}\displaystyle =\displaystyle x+5State the equation
    \displaystyle \left(\sqrt{x+17}\right)^2\displaystyle =\displaystyle \left(x+5\right)^2Square both sides
    \displaystyle x+17\displaystyle =\displaystyle x^2+10x+25Evaluate the exponents
    \displaystyle 0\displaystyle =\displaystyle x^2+9x+8Subtract x and 17 from both sides
    \displaystyle 0\displaystyle =\displaystyle \left(x+1\right)\left(x+8\right)Factor the quadratic

    Using the zero product rule we get two solutions x=-8, x=-1. We now want to test both solutions:

    \displaystyle \sqrt{-8+17}\displaystyle =\displaystyle -8+5Substitute x=-8
    \displaystyle 3\displaystyle =\displaystyle -3Evaluate the addition and square root

    We can see that x=-8 leads to a false statement and is therefore an extraneous solution.

    Now, let's test x=-1.

    \displaystyle \sqrt{-1+17}\displaystyle =\displaystyle -1+5Substitute x=-1
    \displaystyle 4\displaystyle =\displaystyle 4Evaluate the addition and square root

    We can see that x=-1 satisfies the original equation and is a valid solution.

  2. The equation\sqrt{x+17}=x+5 can be written as the system of equations: \begin{cases} y= \sqrt{x+17} \\ y= x+5 \end{cases}

  3. We can use technology to graph the system of equations.

    A screenshot of the GeoGebra geometry tool showing the graphs of y equals square root of x plus 17 and y equals x plus 5. The point of intersection of the graphs is highlighted. Speak to your teacher for more details.
Reflect and check

It is important to note that the fact that our solutions were negative, x=-8, x=-1, does not necessarily make them extraneous. We can see after substitution that only x=- 8 is an extraneous solution and not a point of intersection on the graph of the system of equations, and x=-1 is valid.

Example 3

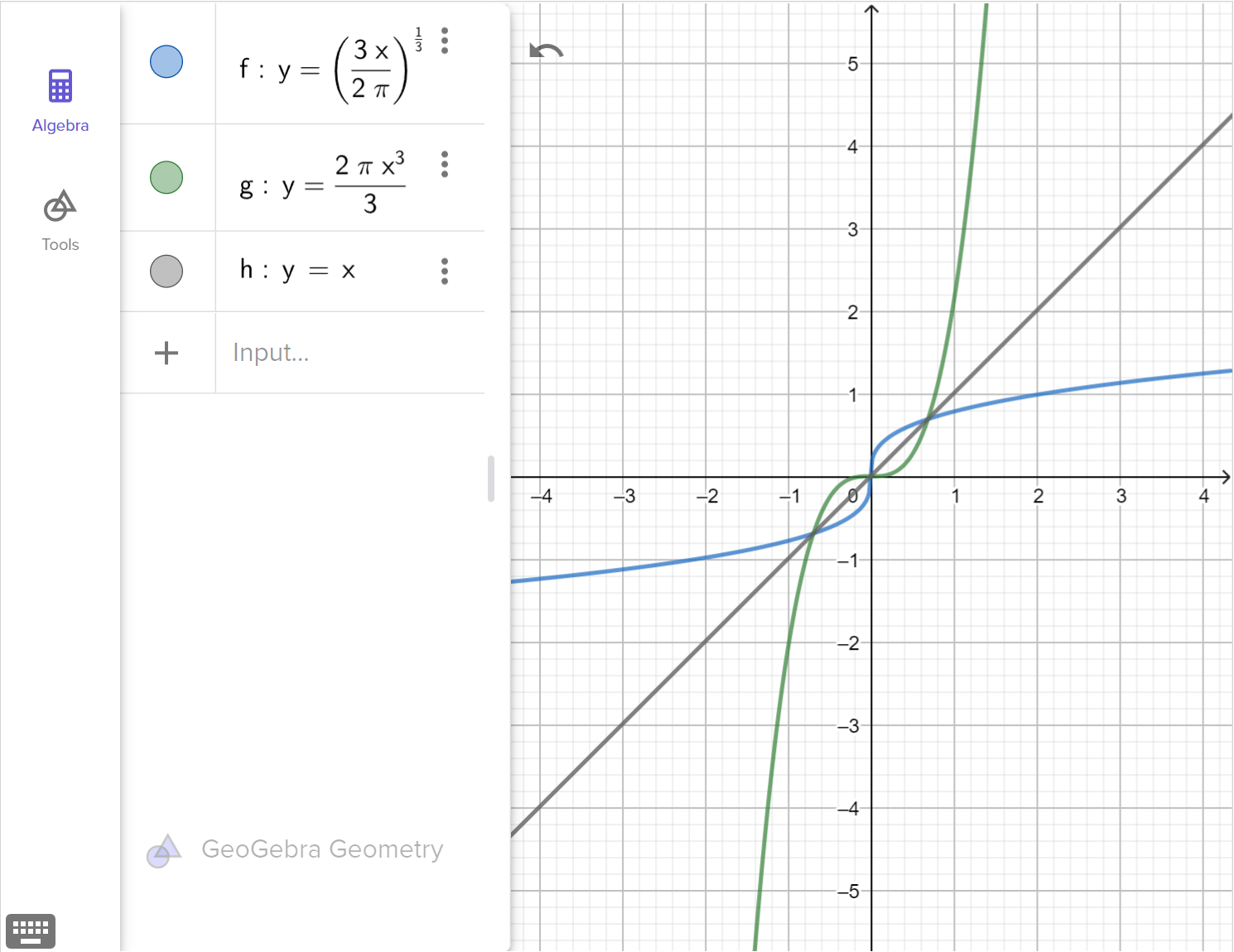
The radius r of a cone whose height is equal to twice its radius is given by r = \sqrt[3]{\dfrac{3V}{2 \pi}}

a

Nirmal is studying an underwater volcano that is roughly this shape. Solve for the volume, V, of the volcano if it has a radius of 1.3\text{ km}. Round your answer to one decimal place.

Worked Solution
Create a strategy

Substitute the radius of the volcano into the formula and solve for V.

Apply the idea
\displaystyle r\displaystyle =\displaystyle \sqrt[3]{\dfrac{3V}{2 \pi}}State the equation
\displaystyle 1.3\displaystyle =\displaystyle \sqrt[3]{\dfrac{3V}{2 \pi}}Substitute r=1.3
\displaystyle 1.3^3\displaystyle =\displaystyle \left(\sqrt[3]{\dfrac{3V}{2 \pi}}\right)^3Cube both sides
\displaystyle 2.197\displaystyle =\displaystyle \dfrac{3V}{2 \pi}Evaluate the cubes
\displaystyle 2.197\left(2 \pi\right)\displaystyle =\displaystyle 3VMultiply by 2 \pi on both sides
\displaystyle \dfrac{2.197\left(2\pi\right)}{3}\displaystyle =\displaystyle VDivide by 3 on both sides
\displaystyle 4.6\displaystyle \approx\displaystyle VEvaluate, rounding to one decimal place

The volcano will have a volume of 4.6\text{ km}^3.

b

Write a function for finding the volume of the volcano for any radius. How are the radius and volume functions related to one another?

Worked Solution
Create a strategy

Solve the equation in terms of V.

Apply the idea
\displaystyle r\displaystyle =\displaystyle \sqrt[3]{\dfrac{3V}{2 \pi}}State the equation
\displaystyle r^3\displaystyle =\displaystyle \dfrac{3V}{2 \pi}Cube both sides
\displaystyle 2 \pi r^3\displaystyle =\displaystyle 3VMultiply both sides by 2 \pi
\displaystyle \dfrac{2 \pi r^3}{3}\displaystyle =\displaystyle VDivide both sides by 3

If we graph the radius and volume functions on the same coordinate plane using technology, we can see that they are reflected across the line y=x and are inverses of each other.

A screenshot of the GeoGebra geometry tool showing the graphs of y equals left parenthesis 3 x over 2 pi right parenthesis raised to one third, y equals 2 pi x cubed all over 3, and y equals x. Speak to your teacher for more details.

Example 4

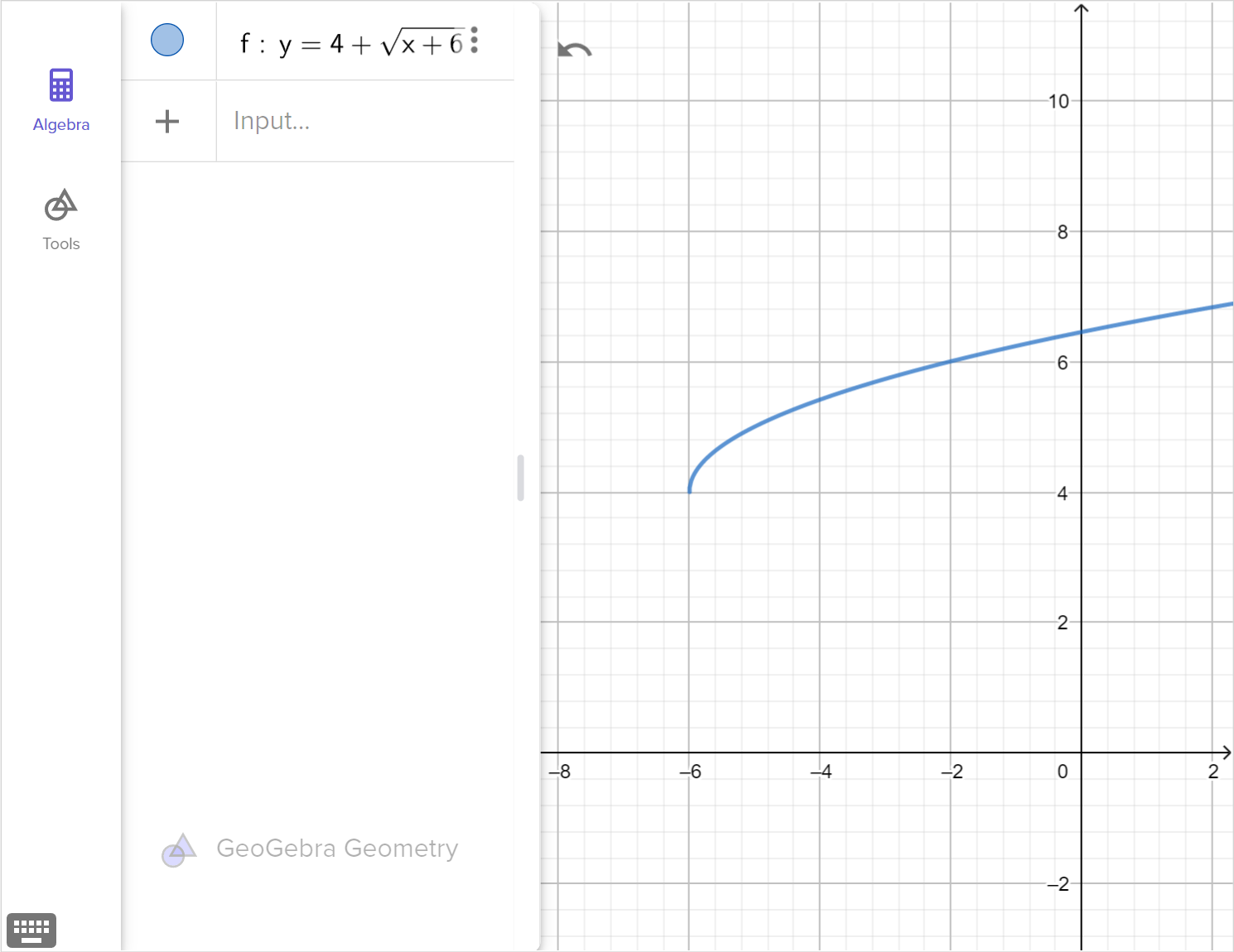
Consider the function f \left( x \right) = 4+\sqrt{x+6}.

a

State the domain and range of f\left(x\right).

Worked Solution
Create a strategy

We can graph the function using technology, then state the domain and range.

A screenshot of the GeoGebra geometry tool showing the graph of y equals 4 plus square root of x plus 6. Speak to your teacher for more details.
Apply the idea

Domain: \left[ - 6 , \infty\right), Range: \left[4, \infty\right)

Reflect and check

We could also have noticed that the function is of the form y=\sqrt{x-h}+k where h=-6 and k=4. This tells us the function has been translated left 6 units and up 4 units.

The domain of the parent function is \left[0,\infty\right), so the domain of the translated function is \left[-6,\infty\right). The range of the parent function is \left[0,\infty\right), so the range of the translated function is \left[4,\infty\right).

b

Find the inverse function f^{ - 1 } \left(x\right).

Worked Solution
Create a strategy

In order to algebraically find the inverse, rewrite the function to include y, then swap x and y and solve for y.

Apply the idea
\displaystyle f \left( x \right)\displaystyle =\displaystyle 4+\sqrt{x+6}Given function
\displaystyle y\displaystyle =\displaystyle 4+\sqrt{x+6}Rewrite the function with y

Inverse:

\displaystyle x\displaystyle =\displaystyle 4+\sqrt{y+6}Swap x and y
\displaystyle x-4\displaystyle =\displaystyle \sqrt{y +6}Subtract 4 from both sides
\displaystyle \left(x-4\right)^2\displaystyle =\displaystyle y+6Square both sides
\displaystyle \left(x - 4\right)^{2} - 6\displaystyle =\displaystyle ySubtract 6 from both sides

The inverse of f \left(x \right) =4 + \sqrt{x + 6} is f^{-1}\left(x\right) =\left(x -4 \right)^2 -6 .

Since the original function's range is \left[4, \infty \right), we know its inverse will be graphed with a domain of \left[4, \infty \right). So, the inverse is f^{-1}\left(x\right) = \left(x-4\right)^2-6 on the restricted domain of \left[4, \infty \right).

Reflect and check

We can check our answer by graphing the original function and the inverse function on the same coordinate plane and verify that they are reflections across the line y=x.

-6
-4
-2
2
4
6
8
10
x
-6
-4
-2
2
4
6
8
10
y
Idea summary

It is important to algebraically substitute solutions into radical equations and identify whether solutions are valid or extraneous.

Outcomes

A.REI.A.2

Solve simple rational and radical equations in one variable, and give examples showing how extraneous solutions may arise.

A.REI.D.11

Explain why the x-coordinates of the points where the graphs of the equations y = f(x) and y = g(x) intersect are the solutions of the equation f(x) = g(x); find the solutions approximately.

F.BF.B.4.A

Solve an equation of the form f(x) = c for a simple function f that has an inverse and write an expression for the inverse.

What is Mathspace

About Mathspace