
Applications of Polynomials
Example 1
Brooklyn Bridge is a cable stayed suspension bridge in New York City. Its construction was one of the industrial wonders of the modern world. The curved cable is parabolic and the approximate dimensions of the bridge within the two massive pylons are indicated in the diagram here:
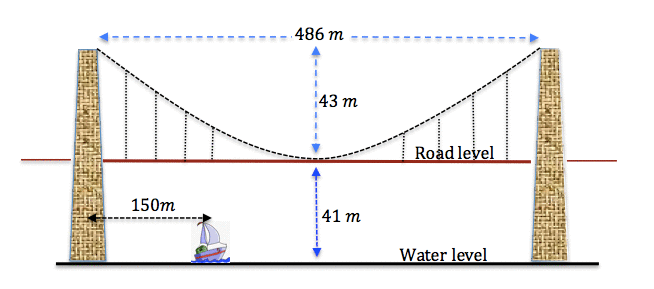
Suppose we have been asked to determine the height above sea-level of the cable at the point directly above a sailing ship that is $150$150 metres in from the left pylon as shown.
We first need to model the suspension cable with a parabola. To do this we imagine an $x$x - axis at water level and a $y$y -axis through the lowest point of the cable, so that we can write coordinates of the lowest cable point as $\left(0,41\right)$(0,41).
Our parabola then has the form $y=ax^2+41$y=ax2+41, and we need to determine the leading coefficient $a$a.
To do this we need another point, and with a little thought, we can ascertain that the coordinate of the point where the cable ties to the top of the right pylon as $\left(243,84\right)$(243,84). This point must satisfy our equation and so:
| $84$84 | $=$= | $a\left(243\right)^2+41$a(243)2+41 |
| $59049a$59049a | $=$= | $43$43 |
| $a$a | $=$= | $\frac{43}{59049}$4359049 |
The value of $a$a is extremely small (approximately $0.000728$0.000728) which makes sense considering that the length of the bridge is about ten times the height at road level.
This means that our cable parabola is given by $y=\left(\frac{43}{59049}\right)x^2+41$y=(4359049)x2+41.
If the ship is $150$150 m from the left pylon, then based on our coordinate system, the $x$x value of the water level point must be given by $x=-\left(243-150\right)=-97$x=−(243−150)=−97. Thus when we substitute this value into our equation we have:
$y=\left(\frac{43}{59049}\right)\left(-97\right)^2+41=47.852$y=(4359049)(−97)2+41=47.852
Hence the cable point directly above the ship is approximately $48$48 metres above sea-level.
Example 2
A cricket ball is fired vertically upwards by a machine so that at time $t$t seconds the height $h$h metres is given by $h=-4.9t^2+39.2t$h=−4.9t2+39.2t. Determine its maximum height.
If we take the common factor $-4.9t$−4.9t out we see that $h=-4.9t\left(t-8\right)$h=−4.9t(t−8). We thus know by setting $h=0$h=0, that the time of flight is $8$8 seconds.
Because a graph of height versus time is an inverted parabola, we know that the maximum height is reached when $t=4$t=4 seconds.
At $t=4$t=4, $h=-4.9\left(4\right)^2+39.2\left(4\right)=78.4$h=−4.9(4)2+39.2(4)=78.4 metres
Example 3
A certain ordered listing of numbers have a sum, up to and including the $n$nth term, given by the formula $S_n=\frac{n}{2}\left(7n-1\right)$Sn=n2(7n−1).
So for example, the list up to the sixth term sums to $S_6=\frac{6}{2}\left(7\times6-1\right)=123$S6=62(7×6−1)=123.
We might ask how many numbers in the list must be added together so that the sum becomes $3348$3348?
We can get a feel for the list by recognising that $S_1=\frac{1}{2}\left(7\times1-1\right)=3$S1=12(7×1−1)=3, and so $3$3 must be the first term of the list.
With $S_2=\frac{2}{2}\left(7\times2-1\right)=13$S2=22(7×2−1)=13 we know therefore that the second term is $10$10, so that $3+10=13$3+10=13. The third term could likewise be revealed as $17$17, and the fourth term $24$24 etc.
The question asks when does $S_n=\frac{n}{2}\left(7n-1\right)=3348$Sn=n2(7n−1)=3348? This is a quadratic equation that can be solved as follows:
| $\frac{n}{2}\left(7n-1\right)$n2(7n−1) | $=$= | $3348$3348 |
| $n\left(7n-1\right)$n(7n−1) | $=$= | $6696$6696 |
| $7n^2-n$7n2−n | $=$= | $6696$6696 |
| $7n^2-n-6696$7n2−n−6696 | $=$= | $0$0 |
| $\left(7n+216\right)\left(n-31\right)$(7n+216)(n−31) | $=$= | $0$0 |
| $n$n | $=$= | $31,-\frac{216}{7}$31,−2167 |
Thus, since $n$n must be positive, $31$31 terms are required so that the sum is $3348$3348.
Worked Examples
QUESTION 1
The sum of the series 1+2+3+...+$n$n is given by $S$S=$\frac{n\left(n+1\right)}{2}$n(n+1)2.
Find the sum of the first $32$32 integers.
Find the number of integers required for a sum of $15$15. (Let the number of integers be $n$n.)
QUESTION 2
Mae throws a stick vertically upwards. After $t$t seconds its height $h$h metres above the ground is given by the formula $h=25t-5t^2$h=25t−5t2.
At what time(s) will the stick be $30$30 metres above the ground?
The stick takes a total of $T$T seconds to hit the ground. Find the value of $T$T.
Can the stick ever reach a height of $36$36 metres?
Yes
ANo
B
QUESTION 3
The arch of a bridge is built so that its height above the horizontal road can be modelled by a parabola whose equation is $y=-\frac{1}{8}\left(x^2-400\right)$y=−18(x2−400), where $y$y represents the height of the arch above the road at distance $x$x metres from the centre of the bridge.

Determine the peak height of the arch.
Pedestrians can climb along the arch up to a point that is horizontally halfway from the centre of the bridge. State the possible $x$x values of this point on the bridge.
Write the two values on the same line separated by a comma.
At this point, how high up are the pedestrians? Give your answer correct to two decimal places.
For what values of $x$x does this model not work?
$x\le-20$x≤−20 and $x\ge20$x≥20
A$x<-20$x<−20 and $x>20$x>20
B$-20$−20 $<$< $x$x $<$< $20$20
C$x<0$x<0
D