
Perpendicular distance
We've looked at the general form of a linear equation, which stated: $ax+by+c=0$ax+by+c=0. We've also looked at how to find the distance between two points on a number plane.
In this chapter, we are going to look at how to find the perpendicular distance from a point to a line, which is the shortest distance between the point and the line.
$d=\frac{\left|ax_1+by_1+c\right|}{\sqrt{a^2+b^2}}$d=|ax1+by1+c|√a2+b2
Proof
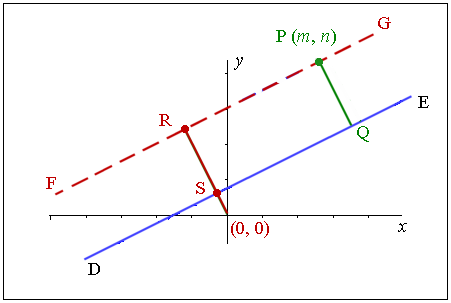
Let's start with the line $Ax+By+C=0$Ax+By+C=0 and label it $DE$DE. It has gradient of $\frac{-A}{B}$−AB.

Now, let's draw on a point $P$P with coordinates $\left(m,n\right)$(m,n). We want to find the perpendicular distance from the point $P$P to the line $DE$DE (that is, the distance of $PQ$PQ).

Now, we're going to draw a second line that is parallel to $DE$DE (so it has the same gradient as $DE$DE) and passes through point $P$P. This line has been labelled $FG$FG.

Now we will construct another line parallel to $PQ$PQ that passes through the origin. This line will have slope $\frac{B}{A}$BA because it is perpendicular to $DE$DE. Let's call this new line $RS$RS.
We will find the distance of $RS$RS, which will be the same distance $PQ$PQ that we wanted at the start.
Ok, now we've done the prep work, let's do some calculations!
Using the point, gradient formula, and rearranging it into general form, we can write the equation of $FG$FG as $y=\frac{-Ax+Am+Bn}{B}$y=−Ax+Am+BnB.
Similarly, line $RS$RS has the equation $y=\frac{B}{A}x$y=BAx.
Now let's find the point of intersection between $FG$FG and $RS$RS by using simultaneous equations.
| $\frac{-Ax+Am+Bn}{B}$−Ax+Am+BnB | $=$= | $\frac{B}{A}x$BAx | Make $x$x the subject of the equation |
| $\frac{A\left(Am+Bn\right)}{A^2+B^2}$A(Am+Bn)A2+B2 | $=$= | $x$x | |
| $x$x | $=$= | $\frac{A\left(Am+Bn\right)}{A^2+B^2}$A(Am+Bn)A2+B2 | (Sub into $y=\frac{B}{A}x$y=BAx) |
| $y$y | $=$= | $\frac{B}{A}\times\frac{A\left(Am+Bn\right)}{A^2+B^2}$BA×A(Am+Bn)A2+B2 | |
| $=$= | $\frac{B\left(Am+Bn\right)}{A^2+B^2}$B(Am+Bn)A2+B2 |
So the coordinates of R are ($\frac{A\left(Am+Bn\right)}{A^2+B^2}$A(Am+Bn)A2+B2,$\frac{B\left(Am+Bn\right)}{A^2+B^2}$B(Am+Bn)A2+B2).
Using this same process, we can conclude that the coordinate of $S$S are $\left(\frac{-AC}{A^2+B^2},\frac{-BC}{A^2+B^2}\right)$(−ACA2+B2,−BCA2+B2).
Now let's use the distance formula to find $RS$RS:
| $d$d | $=$= | $\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}$√(x2−x1)2+(y2−y1)2 |
| $=$= | $\sqrt{\left(\frac{-AC}{A^2+B^2}-\frac{A\left(Am+Bn\right)}{A^2+B^2}\right)^2+\left(\frac{-BC}{A^2+B^2}-\frac{A\left(Am+Bn\right)}{A^2+B^2}\right)^2}$√(−ACA2+B2−A(Am+Bn)A2+B2)2+(−BCA2+B2−A(Am+Bn)A2+B2)2 | |
| $=$= | $\sqrt{\frac{\left(-a\left(Am+Bn+c\right)\right)^2+\left(-B\left(Am+Bn+c\right)\right)^2}{\left(A^2+B^2\right)^2}}$√(−a(Am+Bn+c))2+(−B(Am+Bn+c))2(A2+B2)2 | |
| $=$= | $\sqrt{\frac{\left(A^2+B^2\right)\left(Am+Bn+c\right)}{\left(A^2+B^2\right)^2}}$√(A2+B2)(Am+Bn+c)(A2+B2)2 | |
| $=$= | $\sqrt{\frac{Am+Bn+c}{A^2+B^2}}$√Am+Bn+cA2+B2 |
We can apply the square root but, since distance must be a positive value, will will include the absolute value sign, just in case the numerator is a negative value.
So, the distance from point $\left(m,n\right)$(m,n) to line $Ax+By+C=0$Ax+By+C=0 is given by
$d=\frac{\left|ax_1+by_1+c\right|}{\sqrt{a^2+b^2}}$d=|ax1+by1+c|√a2+b2.
Phew! That was some pretty complex calculations. So let's look at the formula in action using the applet below.
Worked Examples
Question 1
Given a point $\left(x_1,y_1\right)$(x1,y1) and a line $Ax+By+C=0$Ax+By+C=0, what formula can we use to find the perpendicular distance $d$d between the point and the line?
$d=\frac{\left|Ax_1+By_1+C\right|}{\sqrt{A^2-B^2}}$d=|Ax1+By1+C|√A2−B2
A$d=\frac{\left|Ax_1+By_1+C\right|}{\sqrt{A^2+B^2}}$d=|Ax1+By1+C|√A2+B2
B$d=\frac{\left|Ax_1-By_1+C\right|}{\sqrt{A^2+B^2}}$d=|Ax1−By1+C|√A2+B2
C$d=\frac{\left|Ax_1-By_1+C\right|}{\sqrt{A^2-B^2}}$d=|Ax1−By1+C|√A2−B2
D
Question 2
Find the perpendicular distance from the point $\left(-9,-3\right)$(−9,−3) to the line $6x+3y+1=0$6x+3y+1=0
Question 3
If the perpendicular distance from the point $\left(-5,-1\right)$(−5,−1) to the line $-2x-7y+k=0$−2x−7y+k=0 is $\frac{10}{\sqrt{53}}$10√53 what is the value(s) of $k$k?