
Division of an interval in a given ratio
Remember our formula for the midpoint of a line segment?
$x=\frac{x_1+x_2}{2}$x=x1+x22 and $y=\frac{y_1+y_2}{2}$y=y1+y22
When we do this, we are dividing the segment in the ratio $1:1$1:1.
Now, what if we wanted to divide the segment into any ratio we liked? Say, ratio $2:3$2:3? This is our focus for this chapter.
Internal Division of an Interval
Suppose we are given the points $A\left(x_1,y_1\right)$A(x1,y1) and $B\left(x_2,y_2\right)$B(x2,y2) and the interval between them.

What if we are asked to find the point $P\left(x,y\right)$P(x,y) that divides the interval in some given ratio $m:n$m:n, like this?

This is called internal division of an interval in a given ratio and as it turns out, we can derive a formula that breaks down the task of finding $P\left(x,y\right)$P(x,y) into $x$x-coordinates and $y$y-coordinates.
Deriving the Formula
To help us derive our formula, let's firstly notice two things.
Firstly, we can draw perpendicular lines from the axes to our points $A$A,$B$B and $P$P and label their lengths. The vertical lines from the $x$x-axis will have lengths $y_1$y1, $y$y and $y_2$y2 respectively because of the $y$y-coordinates. Similarly, The horizontal lines from the $y$y-axis will have lengths $x_1$x1, $x$x and $x_2$x2 respectively because of the $x$x-coordinates.
Secondly, we can construct two similar right-angled triangles under the interval $AB$AB.

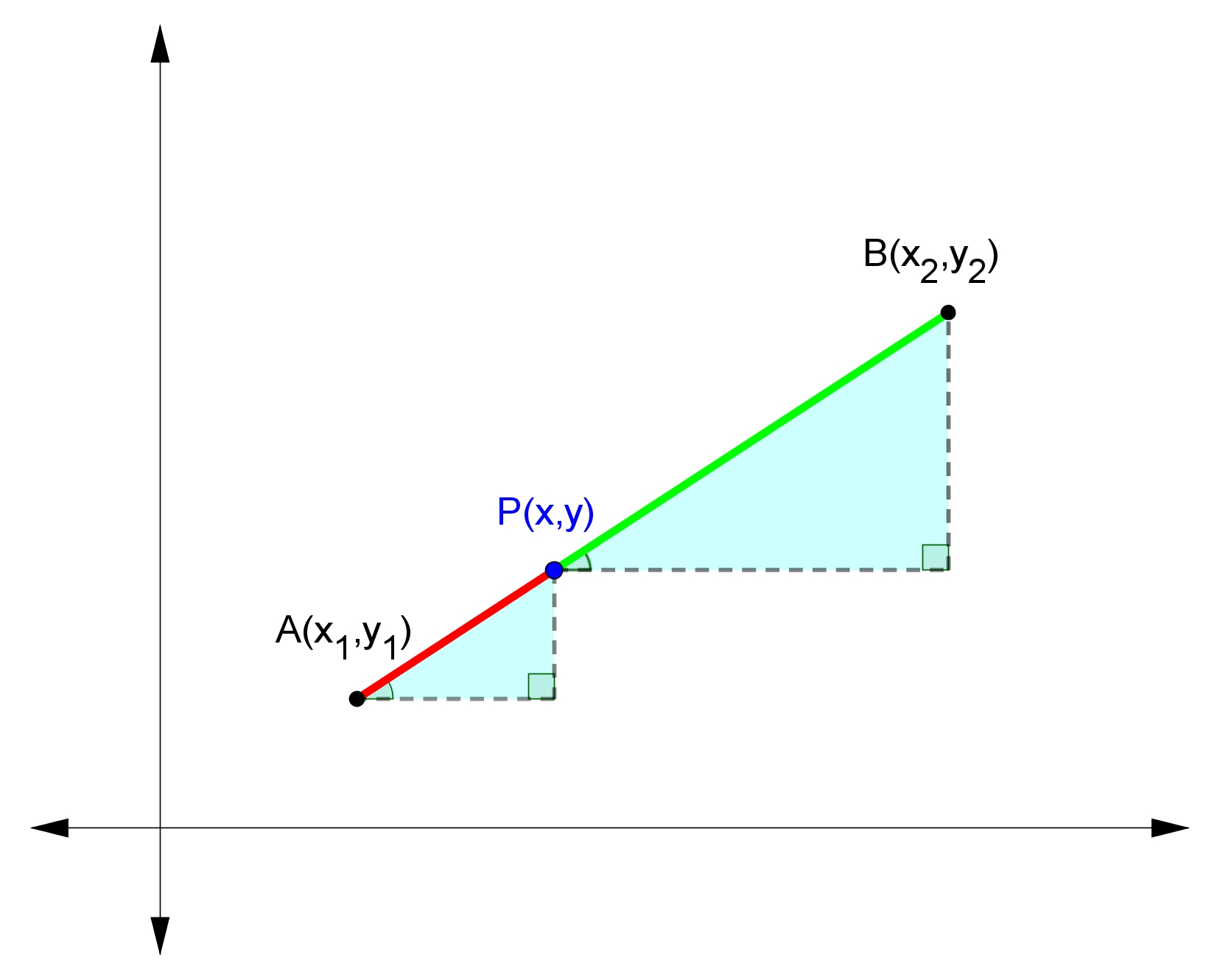
In a similar way to how we derived the distance formula, we can find the side lengths of these similar triangles using the above two images. We simply find the difference between the $x$x-coordinates (shown by the purple dotted lines) to find the horizontal side lengths, and the difference between the $y$y-coordinates (the yellow dotted lines) for the vertical side lengths.


Remember that whenever we have a pair of similar triangles, the lengths of corresponding sides are all going to be in the same proportion.
$\frac{x-x_1}{x_2-x}$x−x1x2−x$=$=$\frac{y-y_1}{y_2-y}$y−y1y2−y$=$=$\frac{m}{n}$mn
We can use this fact to finally get our formulas for the $x$x and $y$y coordinates of $P$P. We use $\frac{x-x_1}{x_2-x}=\frac{m}{n}$x−x1x2−x=mn to derive our formula for the $x$x-coordinate of $P$P.
| $\frac{x-x_1}{x_2-x}$x−x1x2−x | $=$= | $\frac{m}{n}$mn | |
| $n\left(x-x_1\right)$n(x−x1) | $=$= | $m\left(x_2-x\right)$m(x2−x) | Cross multiply |
| $nx-nx_1$nx−nx1 | $=$= | $mx_2-mx$mx2−mx | Expand both sides |
| $mx+nx$mx+nx | $=$= | $mx_2+nx_1$mx2+nx1 | Rearrange |
| $\left(m+n\right)x$(m+n)x | $=$= | $mx_2+nx_1$mx2+nx1 | Factorise the LHS |
| $x$x | $=$= | $\frac{mx_2+nx_1}{m+n}$mx2+nx1m+n | Divide both sides by $\left(m+n\right)$(m+n) |
And similarly, we use $\frac{y-y_1}{y_2-y}=\frac{m}{n}$y−y1y2−y=mn to derive our formula for the $y$y-coordinate of $P$P.
| $\frac{y-y_1}{y_2-y}$y−y1y2−y | $=$= | $\frac{m}{n}$mn | |
| $n\left(y-y_1\right)$n(y−y1) | $=$= | $m\left(y_2-y\right)$m(y2−y) | Cross multiply |
| $ny-ny_1$ny−ny1 | $=$= | $my_2-my$my2−my | Expand both sides |
| $my+ny$my+ny | $=$= | $my_2+ny_1$my2+ny1 | Rearrange |
| $\left(m+n\right)y$(m+n)y | $=$= | $my_2+ny_1$my2+ny1 | Factorise the LHS |
| $y$y | $=$= | $\frac{my_2+ny_1}{m+n}$my2+ny1m+n | Divide both sides by $\left(m+n\right)$(m+n) |
These formulas will work for any two points $A\left(x_1,y_1\right)$A(x1,y1) and $B\left(x_2,y_2\right)$B(x2,y2), and any ratio $m:n$m:n, even if $m$m is larger than $n$n.
Given points $A\left(x_1,y_1\right)$A(x1,y1) and $B\left(x_2,y_2\right)$B(x2,y2), the point that divides the interval $AB$AB internally in the ratio $m:n$m:n is $P\left(x,y\right)$P(x,y), where
$x=\frac{mx_2+nx_1}{m+n}$x=mx2+nx1m+n and $y=\frac{my_2+ny_1}{m+n}$y=my2+ny1m+n
Notice that the formula for the $x$x-coordinate only needs the $x$x-coordinates of $A$A and $B$B, and the formula for the $y$y-coordinate only needs the $y$y-coordinates of $A$A and $B$B.
Pay attention to the order in which the points $A$A and $B$B are given to you! We evaluate the given ratio with respect to the first point given. We can think of the first point given as our 'starting point'.
"Find the point $P\left(x,y\right)$P(x,y) that internally divides the interval joining the points $A\left(a_1,a_2\right)$A(a1,a2) and $B\left(b_1,b_2\right)$B(b1,b2) in the ratio $r_1:r_2$r1:r2"

...is NOT the same as...
"Find the point $P\left(x,y\right)$P(x,y) that internally divides the interval joining the points $B\left(b_1,b_2\right)$B(b1,b2) and $A\left(a_1,a_2\right)$A(a1,a2) in the ratio $r_1:r_2$r1:r2"

In the first example, our starting point is $A$A, and our solution would be given by:
$x=\frac{r_1b_1+r_2a_1}{r_1+r_2}$x=r1b1+r2a1r1+r2 and $y=\frac{r_1b_2+r_2a_2}{r_1+r_2}$y=r1b2+r2a2r1+r2
In the second example, our starting point is $B$B, and our solution would be given by:
$x=\frac{r_1a_1+r_2b_1}{r_1+r_2}$x=r1a1+r2b1r1+r2 and $y=\frac{r_1a_2+r_2b_2}{r_1+r_2}$y=r1a2+r2b2r1+r2
Notice that the $x$x-coordinates $a_1$a1 and $b_1$b1 are switched around, as are the $y$y-coordinates $a_2$a2 and $b_2$b2. This order will affect the result, so read the question carefully!
Examples
Question 1
The point $P$P divides the interval joining the points $A$A$\left(5,10\right)$(5,10) and $B$B$\left(1,2\right)$(1,2) in the ratio $3$3:$1$1.
Find the $x$x-coordinate of $P$P.
Find the $y$y-coordinate of $P$P.
What are the coordinates of $P$P? Express in the form $\left(a,b\right)$(a,b).
Question 2
The interval $AB$AB is divided internally in the ratio $5$5:$3$3 by a point $P$P, where $A$A and $B$B are the points $\left(1,13\right)$(1,13) and $\left(3,11\right)$(3,11) respectively.
Find the $x$x-coordinate of $P$P.
Find the $y$y-coordinate of $P$P.
What are the coordinates of $P$P?
External Division of an Interval
What happens if we use a negative ratio $-m:n$−m:n in our formula? Use the GeoGebra applet below and see!
As it turns out, the point $P\left(x,y\right)$P(x,y) that we get will appear outside of the segment!

The exact same result will occur if we use $m:-n$m:−n, since this is an equivalent ratio, just as the fractions $\frac{-m}{n}$−mn and $\frac{m}{-n}$m−n are equivalent.
How do we make sense of this? Now we can't seem to see $m$m or $n$n on the diagram.
Not to worry. Remember our similar triangles from before? Let's see where those same triangles now sit if $P$P has been dragged backwards past $A$A.

$m$m is still the distance between $A$A and $P$P (now fully outside the interval $AB$AB) and $n$n is still the distance between $B$B and $P$P (now partially outside the interval $AB$AB) but $n$n overlaps with $m$m!


This is called external division of an interval in a given ratio, and the formula remains the same, but our ratio is now negative!
We can think of external division as moving 'backwards' from our given starting point, and then all the way back in the other direction to our other given point.

But be careful! This only works if the size of $m$m is less than the size of $n$n.
If $m$m happens to be larger, $P$P will appear on the other side of the segment!

It's the opposite in this case. We think of moving all the way past our other point to $P$P, and then back to $B$B.

Often we will be given a positive ratio and asked to divide an interval externally with it. In this case, it will be our job to make the ratio negative ourselves! Or, we can change the formula to make the ratio negative, as you'll see below.
Given points $A\left(x_1,y_1\right)$A(x1,y1) and $B\left(x_2,y_2\right)$B(x2,y2), the point that divides the interval $AB$AB externally in the positive ratio $m:n$m:n is $P\left(x,y\right)$P(x,y), where
$x=\frac{mx_2-nx_1}{m-n}$x=mx2−nx1m−n and $y=\frac{my_2-ny_1}{m-n}$y=my2−ny1m−n
Or, if the ratio is already negative, just use the existing formula.
Examples
Question 3
The interval $AB$AB is divided externally in the ratio $4$4:$3$3 by a point $P$P$\left(x,y\right)$(x,y), where $A$A and $B$B are the points $\left(2,9\right)$(2,9) and $\left(3,12\right)$(3,12) respectively.
Find the $x$x-coordinate of $P$P.
Find the $y$y-coordinate of $P$P.
What are the coordinates of $P$P?
$P$P$=$=$\left(\editable{},\editable{}\right)$(,)
Question 4
The point $P$P divides the interval joining the points $\left(-1,10\right)$(−1,10) and $\left(1,11\right)$(1,11) in the ratio $4$4:$3$3.
Find the $x$x-coordinate of $P$P.
Find the $y$y-coordinate of $P$P.
What are the coordinates of $P$P? Express in the form $\left(a,b\right)$(a,b).