
Line and Rotational Symmetries

Symmetry is a pattern of self similarity, and we see symmetry often in the real world. A lot of objects are built with symmetry in mind. There is symmetry in nature, and mathematics has a lot of symmetry as well.
We can define three important types of symmetry: line, point and rotational.
Let's explore what these different symmetries look like using the applet below. (Watch this video if you would like to see this interactive in action - )
Line Symmetry
Line symmetry occurs when a shape or image is reflected across a line. It's like you can fold the shape or image on that line and one side is an exact match of the other.

A popular art activity uses symmetry to create shapes like this butterfly.
The actual line used in line symmetry is also referred to as the axis of symmetry.
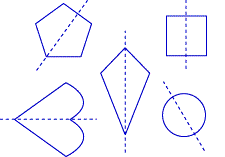
Here are some of the lines of symmetry evident in these geometric shapes. A shape could have more than one line of symmetry. For example, if you have a look at the square or the pentagon, can you see more lines of symmetry?
Rotational Symmetry
Rotational symmetry exists when the shape can be rotated around and the original shape appears again.
See in this shape, as we turn it clockwise, the same external shape appears 3 times in one full rotation. We call this the order of the rotational symmetry. (I coloured the ends so you can see how the shape rotates around.)

Point Symmetry
Point symmetry exists when every point on a shape has a matching point exactly the same distance from a central point.
A circle is an obvious shape with point symmetry because every point on the circumference is the same distance from the centre and is the reflection of another point also on the circumference.
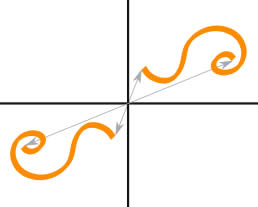
Shapes or images with point symmetry, also have a rotational symmetry of order 2.
Let's have a look at some worked examples.
Question 1
Which of the following letters has rotational symmetry?
Question 2
What type of symmetry do the following shapes have?
Question 3
Deduce whether or not these shapes have point symmetry.