
Rotations on the Cartesian Plane
Rotations
As we saw in the previous lesson on Turns, a rotation occurs when we turn an object or shape around a central point. On the Cartesian plane we usually rotate about the origin, $\left(0,0\right)$(0,0). The object is exactly the same shape and size, just rotated around (like going in a circle). Every point on the object or shape has a corresponding point on the image.
Commonly we describe rotations using a degree measure, and as being either clockwise or anticlockwise.
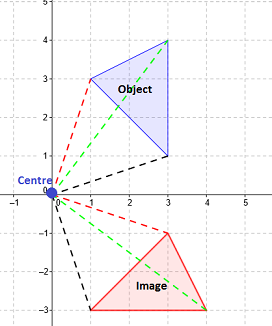
In this example, the image is rotated around the origin by 90 clockwise.
Note how each point creates a 90 degree angle with the origin.
$\left(1,3\right)$(1,3) becomes $\left(3,-1\right)$(3,−1)
$\left(3,1\right)$(3,1) becomes $\left(1,-3\right)$(1,−3)
$\left(3,4\right)$(3,4) becomes $\left(4,-3\right)$(4,−3)
Generally speaking we can see that for a rotation of $90$90 degrees clockwise, that the $\left(a,b\right)$(a,b) becomes $\left(b,-a\right)$(b,−a).
Using the applet below you might like to investigate what happens for rotations of 90°, 180°, 270°, and 360° in both clockwise and anticlockwise directions.
Let's have a look at these worked examples.
Question 1
What is the correct image after Q is rotated $270^\circ$270° clockwise about the origin?
Question 2
a) Graph the points A$\left(5,5\right)$(5,5), B$\left(9,5\right)$(9,5), C$\left(9,9\right)$(9,9) and D$\left(5,9\right)$(5,9).
b) Now plot the points A', B', C' and D' that would result when we rotate the original points A, B, C and D $90^\circ$90° clockwise.
Question 3
a) Plot the points A$\left(-5,-5\right)$(−5,−5), B$\left(-1,-5\right)$(−1,−5), C$\left(-1,-1\right)$(−1,−1) and D$\left(-5,-1\right)$(−5,−1).
b) Now plot the points A', B', C' and D' that would result when we rotate the original points A, B, C and D $90^\circ$90° anticlockwise.