Finding Unknown Angles

We have already seen what the trigonometric ratios are:

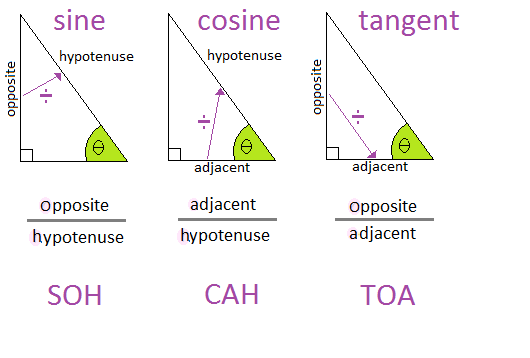
We know wow to calculate with them, and how to find the length of unknown sides of right-angled triangles with them.  

We can also use the trigonometric ratios to find the size of unknown angles.  To do this we need any 2 of the side lengths.

Examples

Question 1

Find the angle indicated in this diagram.

1. label the sides as O, A or H with respect to the position of the angle 

2. Identify the appropriate ratio that uses O and H.  For this question it will be sine (sin)

3. Using algebra, solve the equation for the angle

(write the rule) $\sin\theta=\frac{O}{H}$sinθ=OH​

(fill in what you know)  $\sin\theta=\frac{5}{8}$sinθ=58​

(solve using inverse operations)   $\theta=\sin^{-1}\left(\frac{5}{8}\right)$θ=sin−1(58​)    use a calculator for this bit!

 $\theta=38.68$θ=38.68°

Using the inverse operation for sin/cos/tan 

We looked already at calculating angles from a value, here is a reminder.  

Find $\theta$θ if  $\sin\theta=0.65$sinθ=0.65 answer to $2$2 decimal places

This question is asking us what the angle is if the ratio of the opposite and hypotenuse is $0.65$0.65.  To answer this question you use the inverse sin button on your scientific calculator.  Often it looks a bit like this $\sin^{-1}$sin−1

$\sin\theta=0.65$sinθ=0.65

$\sin^{-1}$sin−1 $0.65=40.54$0.65=40.54°

Question 2

Find the value of the angle indicated.

We have the opposite and adjacent sides here, so the ratio I will use is tangent (tan).

$\tan\theta=\frac{O}{A}$tanθ=OA​              write the rule

$\tan\theta=\frac{14.77}{12.24}$tanθ=14.7712.24​        fill in what we know

$\theta=\tan^{-1}\left(\frac{14.77}{12.24}\right)$θ=tan−1(14.7712.24​)     use inverse operations to rearrange, and then use a calculator

$\theta=50.35$θ=50.35°

Question 3

Question 4

Question 5