
Surface Area of Simple Composite Solids
So we know that surface area is the total area of all the faces on a 3D object. We have looked at surface area of prisms and cylinders.
Sometimes though the shape is a composite solid, (made up of a combination of other solids). These are all composite solids.
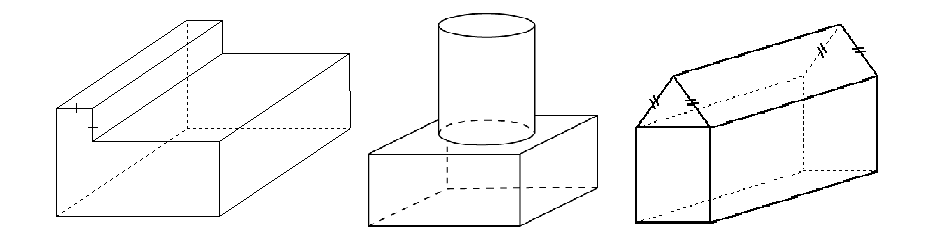
To find the surface area of composite solids we need to be able to visualise the different shapes that make up the various surfaces. Once we have identified the different faces and shapes, calculate the areas of each face and add them up separately.
Don't forget to subtract faces which are not on the surface, like the circle where the cylinder sits on the rectangular prism in the middle image above.
Other common mistakes to be careful about are to not forget faces you may not be able to see in the diagram like those at the back or on the bottom.
Here are some worked examples.
Examples
Question 1
Find the surface area of the figure shown.

Question 2
Find the surface area of the prism shown.
Round your answer to two decimal places.
