13.02 Arithmetics sequences & series
Arithmetic sequences
An arithmetic sequence is a sequence in which the difference between successive terms is a constant. This constant is called the common difference and is usually denoted by the letter $d$d. The common difference, $d$d, is the number that is added to each term to generate the following term. If it seems like the each subsequent term is a result of subtracting the same number from every term then the common difference is negative.
The progression $-3,5,13,21,\ldots$−3,5,13,21,… is an arithmetic sequence with $a_1=-3$a1=−3 and $d=8$d=8. Where $a_1$a1 represents the first term in the sequence. On the other hand, the progression $1,10,100,1000,\ldots$1,10,100,1000,… is not arithmetic because the difference between each term is not constant.
Practice questions
QUESTION 1
Study the pattern for the following sequence, and write down the next two terms.
$6$6, $2$2, $-2$−2, $-6$−6, $\editable{}$, $\editable{}$
QUESTION 2
Study the pattern for the following sequence:
$280,230,180,130,\ldots$280,230,180,130,…
State the common difference between consecutive terms.
QUESTION 3
A diving vessel descends below the surface of the water at a constant rate so that the depth of the vessel after $1$1 minute, $2$2 minutes and $3$3 minutes is $50$50 meters, $100$100 meters and $150$150 meters respectively.
By how much is the depth increasing each minute?
What will the depth of the vessel be after $4$4 minutes?
Continuing at this rate, what will be the depth of the vessel after $10$10 minutes?
Recursive formulas
We can define an arithmetic progression with what is known as a recursive formula. We begin by indicating a first term, $a_1$a1, and then expressing the progression as:
$a_{n+1}=a_n+d,$an+1=an+d, with $a_1$a1 representing the first term of the sequence
So for example, the arithmetic progression given by the recursive equation $a_{n+1}=a_n+\sqrt{2}$an+1=an+√2 with $a_1=1$a1=1 can be constructed term by term as:
$a_2=a_1+\sqrt{2}=1+\sqrt{2}$a2=a1+√2=1+√2
$a_3=a_2+\sqrt{2}=\left(1+\sqrt{2}\right)+\sqrt{2}=1+2\sqrt{2}$a3=a2+√2=(1+√2)+√2=1+2√2
$a_4=a_3+\sqrt{2}=\left(1+2\sqrt{2}\right)+\sqrt{2}=1+3\sqrt{2}$a4=a3+√2=(1+2√2)+√2=1+3√2
From the first four terms, it is clear that the sequence becomes:
$1,1+\sqrt{2},1+2\sqrt{2},1+3\sqrt{2},...,1+\left(n-1\right)\sqrt{2}+...$1,1+√2,1+2√2,1+3√2,...,1+(n−1)√2+...
An interesting sequence is given recursively as $a_{n+1}=a_n+n$an+1=an+n, with $a_1=0$a1=0. To test whether it is an arithmetic sequence, we will consider the first four terms. Here:
$a_1=0$a1=0,
$a_2=a_1+2=2$a2=a1+2=2,
$a_3=a_2+3=2+3=5$a3=a2+3=2+3=5,
$a_4=a_3+4=5+4=9$a4=a3+4=5+4=9,
The differences in successive terms is not constant, but rises by $1$1 each time, so there is a pattern to the sequence, but it is not arithmetic.
Practice questions
Question 4
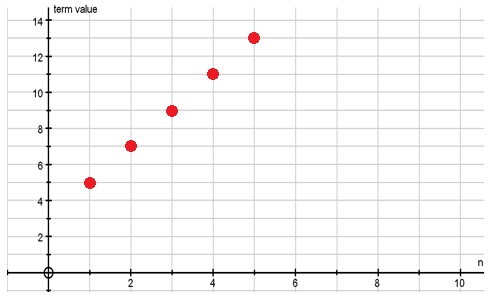
The plotted points represent terms in an arithmetic sequence:
Identify $d$d, the common difference between consecutive terms.
Write a simplified expression for the general $n$nth term of the sequence, $T_n$Tn.
If a line were drawn through the plotted points, what would be the slope of the line?
Question 5
The first term of an arithmetic sequence is $2$2. The fifth term is $26$26.
Solve for $d$d, the common difference of the sequence.
Write a recursive rule for $T_n$Tn in terms of $T_{n-1}$Tn−1 which defines this sequence and an initial condition for $T_1$T1.
Write both parts on the same line separated by a comma.
Question 6
Zuber is a taxi service that charges a $\$1.50$$1.50 pick-up fee and $\$1.95$$1.95 per kilometer of travel.
What is the total charge for a $10$10 km journey?
We want to describe this situation as a recursive sequence.
To start with, state the initial condition $T_0$T0.
Write a recurrence relation for $T_n$Tn in terms of $T_{n-1}$Tn−1 which defines the price of a $n$n km trip.
Explicit formulas
An arithmetic progression starts with a first term, commonly denoted with the variable $a_1$a1 (read "a sub $1$1 because $1$1 is a subscript), and then either increases or decreases by a constant amount called the common difference $d$d. The progression $-3,5,13,21$−3,5,13,21 for example is an arithmetic sequence with $a_1=-3$a1=−3 and $d=8$d=8.
The generating rule for arithmetic sequences follows from this information. Using our example in the first paragraph, we could say that:
the first term is given by $a_1=-3$a1=−3,
the second term is given by $a_2=5=-3+1\times8$a2=5=−3+1×8 ,
the third term is given by $a_3=13=-3+2\times8$a3=13=−3+2×8 ,
the fourth term $a_4=21=-3+3\times8$a4=21=−3+3×8 and so on.
The pattern starts to become clear and we could guess that the tenth term becomes $a_{10}=69=-3+9\times8$a10=69=−3+9×8 and the one-hundredth term $a_{100}=789=-3+99\times8$a100=789=−3+99×8
We could conclude that the generating rule for any arithmetic progression is given by $a_n=a_1+\left(n-1\right)d$an=a1+(n−1)d where $a_n$an is the $n$nth term of the sequence.
In our example we have that $a_n=-3+\left(n-1\right)\times8$an=−3+(n−1)×8 and this can be simplified by distributing the parentheses and collecting like terms as follows:
| $t_n$tn | $=$= | $-3+\left(n-1\right)\times8$−3+(n−1)×8 |
| $t_n$tn | $=$= | $-3+8n-8$−3+8n−8 |
| $t_n$tn | $=$= | $8n-11$8n−11 |
Checking, we see that $a_1=8\times1-11=-3$a1=8×1−11=−3 and that $a_2=8\times2-11=5$a2=8×2−11=5 and that $a_{100}=8\times100-11=789$a100=8×100−11=789.
Trying another example, the decreasing arithmetic sequence $87,80,73,66...$87,80,73,66..., ... has $a=87$a=87 and $d=-7$d=−7. Using our generating formula we have $a_n=87+\left(n-1\right)\times-7$an=87+(n−1)×−7
This simplifies to $a_n=80-7n$an=80−7n and we can use this formula to find any term we like. For example, the first negative term in the sequence is given by $a_{12}=80-7\times12=-4$a12=80−7×12=−4.
Sometimes we are provided with two terms of an arithmetic sequence and then asked to find the generating rule. For example, suppose a certain arithmetic progression has $a_5=38$a5=38 and $a_9=66$a9=66. This mean we can write down two equations:
$a_1+4d=38$a1+4d=38 (1)
$a_1+8d=66$a1+8d=66 (2)
If we now subtract equation (1) from equation (2) the first term in each equation will cancel out to leave us with $\left(8d-4d\right)=66-38$(8d−4d)=66−38. This means $4d=28$4d=28 and so $d=7$d=7.
With the common difference found to be $7$7, then we know that, using equation (1) $a_1+4\times7=38$a1+4×7=38 and so $a_1$a1 is clearly $10$10. The general term is given by $a_n=a_1+\left(n-1\right)d=10+\left(n-1\right)\times7$an=a1+(n−1)d=10+(n−1)×7 and this simplifies to $a_n=3+7n$an=3+7n.
Checking, we see $a_5=3+7\times5=38$a5=3+7×5=38 and $a_9=3+7\times9=66$a9=3+7×9=66.
Practice questions
QUESTION 7
Consider the arithmetic sequence $1.4$1.4$,$, $2.3$2.3$,$, $3.2$3.2$,$, . . . $,$, $10.4$10.4
Determine $d$d, the common difference.
Solve for $n$n, the number of terms in the sequence.
QUESTION 8
The balance of a savings account earning simple interest each year is given by the explicit rule $V_n=2200+300\left(n-1\right)$Vn=2200+300(n−1), where $V_n$Vn is the balance after $n$n years.
How much interest is the account earning each year?
How much is in the account after $1$1 year?
What was the original investment amount?
Write a recurrence relation for $V_n$Vn in terms of $V_{n-1}$Vn−1, and an initial condition $V_0$V0.
Write both parts on the same line, separated by a comma.
Graphical representations
This applet will allow you to explore the geometrical features of an arithmetic sequence, change the values of $a_1$a1 (the initial term) and $d$d (the common difference).
Guiding questions
1. In what ways is the formula for an arithmetic sequence similar to the equation of a line?
2. In what ways is the graph of an arithmetic sequence similar to the graph of a line?
Think about the generating rule for a particular arithmetic sequence given by $a_n=2n+3$an=2n+3. We can cleverly rearrange this equation to $a_n=5+\left(2n-2\right)$an=5+(2n−2) . By taking out common factors on the last two terms, the expression becomes:
$a_n=5+\left(n-1\right)\times2$an=5+(n−1)×2
Comparing this to the general formula for the $n$nth term of an AP, given by $a_n=a+\left(n-1\right)d$an=a+(n−1)d , we can immediately see that the first term is $5$5 and the common difference is $2$2.
Thus any generating rule of the form $a_n=dn+k$an=dn+k where $d$d and $k$k are constants can be shown to be an arithmetic sequence. Just like the equation $y=mx+c$y=mx+c is drawn as a straight line, so the arithmetic progression given by $a_n=dn+k$an=dn+k is plotted as a series of points that are all in a straight line.
The first term is represented by the left-most point shown $\left(t_1=5\right)$(t1=5) . The slope of the marked points measured, as the vertical distance between the points, is the common difference. In our example, the line of points is rising, so this indicates a positive common difference. In other instances, the line might be falling and this would indicate a negative common difference.
Practice questions
QUESTION 9
The plotted points represent terms in an arithmetic sequence:
Complete the table of values for the given points.
$n$n $1$1 $2$2 $3$3 $4$4 $T_n$Tn $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Identify $d$d, the common difference between consecutive terms.
Write a simplified expression for the general $n$nth term of the sequence, $T_n$Tn.
Find the $15$15th term of the sequence.
QUESTION 10
For a fiber-optic cable service, Christa pays a one off amount of $\$200$$200 for installation costs and then a monthly fee of $\$30$$30.
Complete the table of values for the total cost $\left(T\right)$(T) of Christa's service over $n$n months.
$n$n $1$1 $2$2 $3$3 $4$4 $18$18 $T$T $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ By how much are consecutive terms in the sequence increasing?
Considering the table of values, plot the points corresponding to $n=1$n=1, $n=2$n=2, $n=3$n=3 and $n=4$n=4.
Loading Graph...If the points on the graph were joined, they would form:
a straight line
Aa curved line
B
QUESTION 11
The values in the table show the $n$nth term in an arithmetic sequence for consecutive values of $n$n.
Complete the missing values in the table.
$n$n $1$1 $2$2 $3$3 $4$4 $5$5 $T_n$Tn $-6$−6 $\editable{}$ $\editable{}$ $\editable{}$ $-26$−26
Practical applications
There is a range of everyday applications involving arithmetic sequences. If you are saving money in equal installments, for example, the cumulative savings at each savings period form an arithmetic sequence. If you are traveling down a highway at a constant speed, the amount of gasoline left in the tank, if measured every minute of the trip, forms another arithmetic progression. In fact any time you notice a quantity changing in equal amounts at set time periods, then you can consider that process as being arithmetic.
Tackling problems involving arithmetic sequences can often be made easier by generalizing the process by constructing a formula. Suppose for example a wealthy Chief Executive Officer decides to save an amount of $\$25$$25 birthday money given to her, but then adds to it according to the following plan. On the day after her birthday she will add a further $\$26$$26 to the savings. On day two, she will add another $\$27$$27 and again on day three she will add $\$28$$28, continuing on in this manner until the day before her next birthday. How much will the CEO have all together?
Such a problem could be answered by carefully adding up the installments day by day until the total is obtained. Not only is this time consuming, we might suspect our answers accuracy given the $365$365 additions required. Moreover, while the specific problem might be solved, we would need to repeat the procedure for any other similar problem. We will not have learned anything about the general features of the savings construction. Developing a formula on the other hand may reveal a type of generality that may be very useful in solving a range of similar problems.
Taking this general approach we might see the problem is arithmetic, and set $a_1=250$a1=250 and $d=1$d=1 then using the formula for the $n$nth term of an AP, given as $a_n=a_1+\left(n-1\right)d$an=a1+(n−1)d, we determine the rule for this particular process is
| $a_n$an | $=$= | $25+\left(n-1\right)\times1$25+(n−1)×1 |
| $=$= | $n+24$n+24 |
The last term of the finite sequence corresponding to the amount saved on the day before her birthday is thus $a_{365}=365+24=389$a365=365+24=389. This means that the sum of the savings sequence $25,26,27,...,389$25,26,27,...,389 can be determined using the the arithmetic sum formula $S_n=\frac{n}{2}\left(a+l\right)$Sn=n2(a+l) .
In our problem we determine specifically that
| $S_{365}$S365 | $=$= | $\frac{365}{2}\left(25+389\right)$3652(25+389) |
| $=$= | $75555$75555 |
and so the total amount saved in the year is $\$75555$$75555.
We could ask a different question about the specific savings plan the CEO has constructed. We might for example ask how long it would take for the savings to reach $\$10100$$10100. That is, we are asking for what specific value of $n$n will $S_n=10100$Sn=10100. To answer this recall that the sum of an arithmetic progression can also be expressed as $S_n=\frac{n}{2}\left[2a+\left(n-1\right)d\right]$Sn=n2[2a+(n−1)d]. Putting in the specific parameters for this problem, we see that
| $S_n$Sn | $=$= | $\frac{n}{2}\left[2\times50+\left(n-1\right)\times1\right]$n2[2×50+(n−1)×1] |
| $=$= | $\frac{n}{2}\left(99+n\right)$n2(99+n) |
Thus we can solve the problem by setting $\frac{n}{2}\left(99+n\right)=10100$n2(99+n)=10100. This is a quadratic equation and could be solved by rearranging first and then using factoring techniques. However if we look carefully at the equation, we might see that $n=101$n=101 days is an obvious solution. In other instances we may not be so lucky.
Also note that our formula provides the opportunity to find intermediate savings states. For example, $99$99 days on from the CEO's birthday, we can easily determine that $a_{100}=124$a100=124 and thus
| $S_{100}$S100 | $=$= | $\frac{100}{2}\left(25+149\right)$1002(25+149) |
| $=$= | $8700$8700 |
or $\$8700$$8700. Also, note that any other arithmetic savings plan can be interrogated in the same way.
Practice questions
QUESTION 12
A diving vessel descends below the surface of the water at a constant rate so that the depth of the vessel after $4$4 minutes, $8$8 minutes and $12$12 minutes is $5$5 meters, $10$10 meters and $15$15 meters respectively.
If $n$n is the number of minutes it takes to reach a depth of $40$40 meters, solve for $n$n.
QUESTION 13
Bart is learning to drive. His first lesson is $26$26 minutes long, and each subsequent lesson is $4$4 minutes longer than the lesson before.
How long will his $15$15th lesson be?
If Bart reaches $9.6$9.6 total hours of driving on his $n$nth lesson, solve for $n$n.
QUESTION 14
Katrina starts training for a $4.5$4.5 km charity trail run by running every week for $28$28 weeks.
She runs $2$2 km of the course in the first week, and each week after that she runs $250$250 meters more than the previous week.
She continues to increase the distance she runs until the week when she runs far enough to complete the course. Each week after that she completes the course without increase.
How far does she run in the $11$11th week? Give your answer correct to two decimal places, if necessary.
What is the total distance that Katrina runs in $28$28 weeks? Give your answer correct to two decimal places, if necessary.
Arithmetic series
Suppose we wanted to add all of the terms in an arithmetic sequence together. We'd be finding what's known as an arithmetic series.
Exploration
If the first term of an arithmetic sequence is $a_1$a1 and the common difference is $d$d , then the sequence becomes:
$a_1$a1 , $a_2=a_1+d$a2=a1+d , $a_3=a_1+2d$a3=a1+2d , $a_4=a_1+3d$a4=a1+3d , $a_5=a_1+4d$a5=a1+4d, ...
Suppose we continue writing the terms all the way up to $a_{100}=a_1+99d$a100=a1+99d , and then find a way to add up all of the one hundred terms together. The great German mathematician Carl Friedrich Gauss in 1785, at the age of 8 years old, used the following method.
Instead of adding the terms from left to right, he added them in this order:
$\left(t_1+t_{100}\right)+\left(t_2+t_{99}\right)+\left(t_3+t_{98}\right)+$(t1+t100)+(t2+t99)+(t3+t98)+ $...+\left(t_{48}+t_{52}\right)+\left(t_{49}+t_{51}\right)$...+(t48+t52)+(t49+t51)
Can you see why he may have done that?
Every grouped pair of terms adds up to $2a_1+99d$2a1+99d and since there are fifty pairs, their total must be $50\times\left(2a_1+99d\right)$50×(2a1+99d). Gauss knew there were $50$50 pairs because there are $100$100 terms. His answer could be written $\frac{100}{2}\times\left(2a_1+99d\right)$1002×(2a1+99d) .
This led him to consider a formula for adding any number of terms of any arithmetic sequence. Writing $S_n$Sn for the sum to $n$n terms, Gauss was able to show that:
$S_n=\frac{n}{2}\left[2a_1+\left(n-1\right)d\right]$Sn=n2[2a1+(n−1)d]
The sum of a finite arithmetic series with $n$n terms, denoted $S_n$Sn , or the $n$nth partial sum of an arithmetic series can be found using one of the two related formulas:
$S_n=\frac{n}{2}\left[2a_1+\left(n-1\right)d\right]$Sn=n2[2a1+(n−1)d]
$S_n=\frac{n}{2\left(a_1+a_n\right)}$Sn=n2(a1+an)
Worked example
Question 15
Evaluate the sum of all the positive integers from $1$1 to $49$49.
Think/Do: With $a_1=1$a1=1 and $d=1$d=1 we have:
$S_{49}=\frac{49}{2}\left[2\times1+\left(49-1\right)\times1\right]=1225$S49=492[2×1+(49−1)×1]=1225
Reflect: Note that the formula works even though there is an odd number of terms to add up. Can you explain why?
Practice questions
QUESTION 16
Find the sum of the first $10$10 terms of the arithmetic sequence defined by $a=6$a=6 and $d=3$d=3.
QUESTION 17
The first term of an arithmetic sequence is $-5$−5 and the $6$6th term is $-45$−45.
If $d$d is the difference between terms, solve for $d$d.
Hence, find the sum of the first $14$14 terms.
QUESTION 18
Find the sum of the first $10$10 terms of the arithmetic sequence defined by $T_4=4$T4=4 and $T_7=13$T7=13.