11.02 Operations with vectors
Addition of vectors
Vectors can be added together. To do this, we use what is called the top to tail method. We put the head of the second vector on top of the tail of the first and the resultant vector (of the result of adding the two vectors together) is the vector that reaches from the initial point of the first, to the terminal point of the second. So adding vectors $u$u and $v$v below, results in $w$w.

So geometrically this is what is happening with vector addition, let's know look at the algebraic process.
For this I am going to use the column vector notation. Remember that the first element in the column matrix indicates the $x$x movement (right is positive and left is negative) and the second element indicates the change in $y$y, (up positive and down negative).

Using column vector notation, makes adding vectors a relatively simple process akin to adding column matrices. We just added the corresponding elements together.
Let's look at what happened geometrically with the same vector addition.
Here vectors $u$u and $v$v are drawn.

We can see that the matrix components above, relate directly to the $x$x and $y$y components of these vectors.

To add together, we reposition vector $v$v so that the head of $v$v, is positioned at the tail of $u$u.

The resultant vector is the vector that extends from the beginning of $u$u, and ends at the tail of $v$v.

This vector has $x$x and $y$y components as shown here.

And this is the same as the matrix result we had earlier.
Using column vector notation, makes adding vectors a relatively simple process akin to adding column matrices. We just added the corresponding elements together. Thus, using this process, we can add any number of vectors together.
This applet will allow you to create vectors of given sizes, and then demonstrate their additions geometrically.
Practice questions
Question 1
Which vector is the result of $a+b$a+b?
$c$c
A$d$d
B
Question 2
Consider the two vectors $a$a and $b$b, as graphed below.
Plot the result of $a+b$a+b on the same axes.
Loading Graph...Now plot the result of $b+a$b+a.
Loading Graph...Are the two resulting vectors $a+b$a+b and $b+a$b+a equal?
Yes
ANo
B
Question 3
Consider vectors $U$U and $V$V with magnitudes $\left|U\right|=35$|U|=35 and $\left|V\right|=75$|V|=75 units, separated by an angle of $90^\circ$90°. Let $W=U+V$W=U+V be the resultant vector.
Calculate the magnitude of $W$W, correct to three decimal places:
Find the angle between the resultant $W$W and $U$U in degrees, correct to two decimal places:
Subtraction of vectors
Subtracting vectors combines the ideas of negative vectors and addition.
Remember how a negative vector has same size but opposite direction, well this means that the concept of subtracting a vector is the same as adding its negative.
That is that
$a-b=a+(-b)$a−b=a+(−b)
Geometrically it looks like this
here are vectors $u$u and $v$v
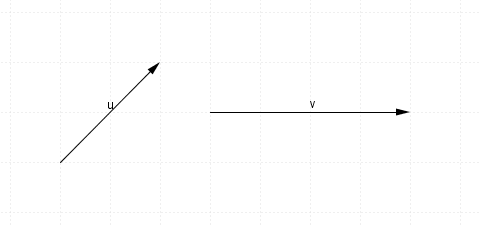
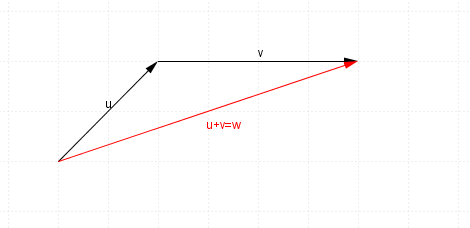
$u+v$u+v will look like this (remember to head to tail it)
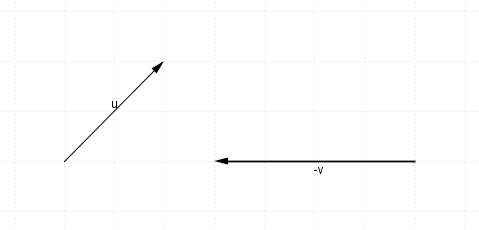
$-v$−v will look like this, (same size as $v$v, just opposite direction)
and hence $u-v$u−v, or $u+-v$u+−v will look like this
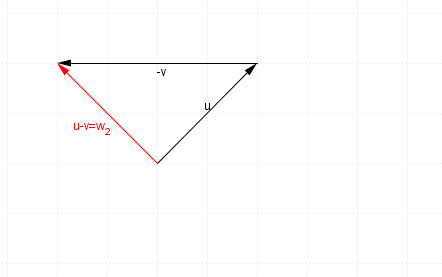
Here are both situations to compare on the one diagram
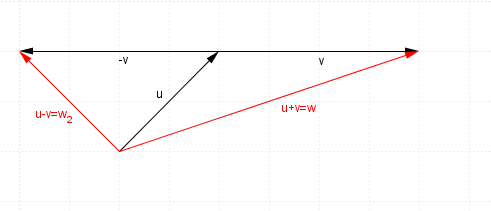
Of course if we use matrix notation, then this becomes a simple process of matrix subtraction.
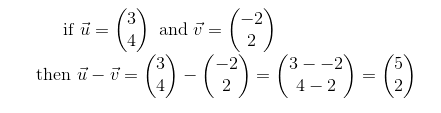
This applet will allow you to practice making vectors, and then demonstrate their subtraction via a geometric representation.
Practice question
Question 4
| Consider the vectors $a$a$=$= |
|
and $b$b$=$= |
|
. |
Find $a-b$a−b.
$a-b$a−b $=$= $\editable{}$ $\editable{}$ Find $\left|a-b\right|$|a−b|.
Applications of addition and subtraction
The development of vector methods in school mathematics is motivated initially by problems involving the vector quantities force, displacement, velocity and the like.
In this chapter, we consider problems of this sort but it is worth mentioning that there are many other objects that can be treated as vectors and the theory of vector spaces has applications in diverse fields. Consider, for example, the computer software that finds the best fitting line or curve to a given set of bivariate data. This is an application of vector mathematics in statistics, where the vectors are the columns of data.
We begin with problems from physics.
Worked examples
Question 5
A small boat sails a distance of $12$12 km on a bearing $030^\circ$030° and then turns to bearing $250^\circ$250° and travels a further $10$10 km. How far from its starting point is the boat and what should its bearing be to return there?
This problem can be solved using the sine and cosine rules in trigonometry but we will use a vector approach.
The first diagram below represents the problem as it might appear on a map. The second diagram shows the displacements as vectors in coordinate form.


We used some simple trigonometry to obtain the coordinates of the displacement vectors. The resultant vector, in red, should be the sum of the two displacements. Its coordinate representation is
$\left(12\cos60^\circ-10\cos20^\circ,12\sin60^\circ-10\sin20^\circ\right)$(12cos60°−10cos20°,12sin60°−10sin20°)
This simplifies to $\left(-3.40,6.97\right)$(−3.40,6.97). This vector has length $\sqrt{(-3.40)^2+(6.97)^2}\approx7.76$√(−3.40)2+(6.97)2≈7.76. So, the boat has a return journey of $7.76$7.76 km.
The bearing angle of the red arrow is $\arctan\left(\frac{6.97}{-3.4}\right)\approx296^\circ$arctan(6.97−3.4)≈296°. So, for the return trip, the bearing will need to be $180^\circ$180° away from this, which is $116^\circ$116°.
Question 6
A $20$20 kg mass is suspended on a chain $A$A attached to a ceiling timber. This means that there is a tension force of $20\times9.8$20×9.8 N in the chain when it is hanging vertically (if we ignore the weight of the chain).
Suppose the $20$20 kg mass is pulled horizontally by another chain $B$B until the chain attached to the ceiling is at an angle of $20^\circ$20° from the vertical. Has the tension in chain $A$A increased?
What are the tension forces in the two chains?
We make use of the fact that the vector with magnitude $T_A$TA can be resolved into two orthogonal components. These are shown as green arrows. If the two green arrows acted, they would have the same effect as the red arrow with magnitude $T_A$TA alone. In effect, we replace it by the pair of components.

The diagram illustrates the setup. Since $T_A>T_A\cos20^\circ$TA>TAcos20°, and this vertical force, magnitude $T_A\cos20^\circ$TAcos20°, is balancing the weight force of $196$196 N, we conclude that the tension in chain $A$A is greater than when the weight was hanging vertically.
We form two equations:
$T_A\cos20^\circ+196=0$TAcos20°+196=0
$T_B+T_A\sin20^\circ=0$TB+TAsin20°=0
From the first of these we find $T_A=\frac{-196}{\cos20^\circ}=-208.6$TA=−196cos20°=−208.6 N. We have taken the downward weight force to be positive. So, this tension force acts upward.
Then, from the second equation, we obtain $T_B=-(-208.6)\sin20^\circ=71.3$TB=−(−208.6)sin20°=71.3 N.
As an alternative strategy, we might note that in coordinate form the vector with magnitude $T_A$TA is $\left(T_A\sin20^\circ,T_A\cos20^\circ\right)$(TAsin20°,TAcos20°). The weight vector is $(0,-196)$(0,−196) and the sideways pull $T_B$TB is $\left(T_B,0\right)$(TB,0).
These three vectors should add to the zero vector $(0,0)$(0,0). So, we have $\left(T_A\sin20^\circ+0+T_B,T_A\cos20^\circ-196+0\right)=(0,0)$(TAsin20°+0+TB,TAcos20°−196+0)=(0,0). This vector equation leads to the same two equations as we derived above.
Question 7
A river flows at the rate of $0.5$0.5 m/s. A swimmer starting from the river bank aims at the opposite side and maintains a speed of $1.26$1.26 m/s in a direction perpendicular to the flow of the river. What is the swimmer's velocity (magnitude and direction) relative to the river bank?
The swimmer will be swept downstream. The vector representing the swimmer's motion will be the sum of $(0.5,0)$(0.5,0) and $(0,1.26)$(0,1.26). That is, the vector with coordinate form $(0.5,1.26)$(0.5,1.26). The magnitude of this vector is $\sqrt{0.5^2+1.26^2}\approx1.36$√0.52+1.262≈1.36 m/s.
The angle of the motion from the river bank is $\arctan\left(\frac{1.26}{0.5}\right)\approx68.4^\circ$arctan(1.260.5)≈68.4°.
Suppose now that the swimmer wishes to maintain a course directly towards the opposite bank. The swimmer will need to swim upstream at a certain angle to the river bank to achieve this. What is the angle and what will be the swimmer's velocity in the direction directly across the river?
For the moment, we express the vector representing the swimmer's motion relative to the river bank by $(x,y)$(x,y), where $x=1.26\cos\theta$x=1.26cosθ and $y=1.26\sin\theta$y=1.26sinθ. It must be that the river flow vector and the cross stream vector sum to this vector. So, $(0.5,0)+(0,v)=(x,y)$(0.5,0)+(0,v)=(x,y) where $v$v is the magnitude of the resultant velocity across the stream.
Thus, we can form the equations
$0.5+0=1.26\cos\theta$0.5+0=1.26cosθ and
$0+v=1.26\sin\theta$0+v=1.26sinθ
From the first equation, we deduce that $\theta=66.6^\circ$θ=66.6°. Then, from the second equation, $v=1.26\times\sin66.6^\circ\approx1.16$v=1.26×sin66.6°≈1.16 m/s.
Practice questions
Question 8
Question 9
Kenneth wants to fly his plane due north at $410$410 km/h relative to the ground. If a $80$80 km/h wind is blowing from the north-west, what velocity in the air should he fly his plane?
Give your answer in terms of the unit vectors $i$i and $j$j, where north corresponds to the positive $y$y direction.
Question 10
An elite military unit is trekking a forest to capture an enemy soldier who is hiding in the forest. They travel $150$150 m north-east and then $250$250 m south. Once there, they turn $150^\circ$150° clockwise and travel $90$90 m, at which point they spot the soldier.
What is the displacement of the soldier from their starting point?
Give your answer in terms of $i$i and $j$j, where the components are correct to two decimal places.
Find the magnitude of the displacement.
Find $\theta$θ, the acute angle between the displacement and due east.
Give your answer to the nearest tenth of a degree.
Hence find the true bearing of the soldier.
Scalar multiplication of vectors
As a scalar is a quantity that is magnitude only (no direction), its affect on a vector when multiplying is to increase the magnitude of the vector. It does not alter its direction.
Scalar multiplication of vectors can be done geometrically (like in the applet above), where we draw the resulting vector with the scaled magnitude and same direction. But it can also be done algebraically using column vector notation.
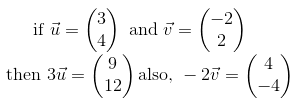
Note also how a negative scalar multiple is actually a negative of the vector (same magnitude opposite direction) and then it is scaled according to the scalar quantity.
Familiarize yourself with the behavior of scalar multiplication.
c and d scalars, $v$v and $w$w vectors
- Left distributivity: (c+d)$v$v=c$v$v+d$v$v
- Right distributivity: c($v$v+$w$w)=c$v$v+c$w$w
- Associativity: (cd)$v$v=c(d$v$v)
- Mutliplying by 1 does not change a vector: 1$v$v=$v$v
- Multiplying by 0 gives the zero vector: 0$v$v=0
- Multiplying by -1 gives the additive inverse: (-1)$v$v=-$v$v
Construct examples (using diagrams and algebra), that demonstrate each of these properties.
Practice questions
Question 11
Consider the vectors shown below.
|
Loading Graph... |
Loading Graph... |
|
Loading Graph... |
Loading Graph... |
Which vector is equivalent to $2a$2a?
$a$a
A$b$b
B$c$c
C$d$d
DWhich vector is equivalent to $\frac{1}{4}b$14b?
$a$a
A$b$b
B$c$c
C$d$d
DWhich vector is equivalent to $-a$−a?
$a$a
A$b$b
B$c$c
C$d$d
DWhich vector is equivalent to $-\frac{1}{2}d$−12d?
$a$a
A$b$b
B$c$c
C$d$d
D
Question 12
| Let $a$a$=$= |
|
. Using the origin as the starting point, plot the following vectors: |
$3a$3a
Loading Graph...$-2a$−2a
Loading Graph...$\frac{1}{2}a$12a
Loading Graph...
Magnitudes of scalar multiples
Having looked at magnitudes of vectors, and scalar multiples of vectors we can combine these to find the magnitude of scalar multiples.
![]() represents the magnitude of
represents the magnitude of ![]() . We can calculate it using Pythagoras' theorem.
. We can calculate it using Pythagoras' theorem.
A scalar multiple is found by extending the length of ![]() by a multiple, let's call $k$k. So it makes sense then that the magnitude of the scalar multiple is a scalar multiple of the magnitude.
by a multiple, let's call $k$k. So it makes sense then that the magnitude of the scalar multiple is a scalar multiple of the magnitude.

If the vector was defined using column matrix notation, then

Let's find the magnitude of the vector pictured, after it is scaled by a multiple of $3$3.

Method 1 - Find the magnitude then scale it by $3$3.
Magnitude of $u$u
$\left|u\right|=\sqrt{2^2+\left(-6\right)^2}=\sqrt{40}=2\sqrt{10}$|u|=√22+(−6)2=√40=2√10
Then scale by $3$3, so magnitude of $3u$3u
$3\times\left|u\right|=3\times2\sqrt{10}=6\sqrt{10}$3×|u|=3×2√10=6√10
Method 2 - Find the new scaled vector, then find that magnitude.
$3u$3u will be $$
Now find the magnitude of this
$\sqrt{6^2+\left(-18\right)^2}=\sqrt{360}=6\sqrt{10}$√62+(−18)2=√360=6√10
Both answers yield the same result.