2.02 Polynomial functions

Polynomial curve sketching

Certain polynomials of degree $n$n can be factored into $n$n linear factors over the real number field.

For example the $4$4th degree polynomial $P\left(x\right)=2x^4-x^3-17x^2+16x+12$P(x)=2x4−x3−17x2+16x+12 can be re-expressed as $P\left(x\right)=\left(x+3\right)\left(2x+1\right)\left(x-2\right)^2$P(x)=(x+3)(2x+1)(x−2)2. Note that there are two distinct factors, the $\left(x+3\right)$(x+3) and $\left(2x+1\right)$(2x+1) and two equal factors, the $\left(x-2\right)$(x−2) appears twice.

A polynomial function $y=P\left(x\right)$y=P(x) that can be completely factored into its linear factors can be easily sketched. The function $y=\left(x+3\right)\left(2x+1\right)\left(x-2\right)^2$y=(x+3)(2x+1)(x−2)2 has roots immediately identifiable as $x=-3,-\frac{1}{2}$x=−3,−12​ and $x=2$x=2.

Multiplicity

A root is said to have multiplicity $k$k if a linear factor occurs $k$k times in the polynomial function. For example the function of degree $6$6 given by $y=\left(x-1\right)\left(x+1\right)^2\left(x-2\right)^3$y=(x−1)(x+1)2(x−2)3 is said to have a root $x=1$x=1 of multiplicity $1$1 (a single root), another root of $x=-1$x=−1 of multiplicity $2$2 (a double root or two equal roots) and a root $x=2$x=2 of multiplicity $3$3 (a triple root or three equal roots). In effect that is $6$6 roots all together.

The key to understanding how a root's multiplicity effects the graph is given in the following statement:

The curve's shape near a root depends on the root's multiplicity.

Look closely at the sketch of $y=\left(x-1\right)\left(x+1\right)^2\left(x-2\right)^3$y=(x−1)(x+1)2(x−2)3

 

The curve approaching a root of multiplicity $1$1 will behave like a linear function across that root (see position B on graph). The curve approaching a root of multiplicity $2$2 will behave like a quadratic function across that root (see position A on graph). The curve approaching a root of multiplicity $3$3 will behave like a cubic function across that root (see position C on graph).

In general, the curve approaching a root of multiplicity $k$k will behave like the function $y=x^k$y=xk across that root.

There is also two other considerations that will help with the graphing of the function.

Firstly, note that this function is an even degree function, so at the left and right extremes it will move away from the $x$x - axis in the same direction. Odd degree functions move away in opposite directions.

Secondly, because the coefficient of the greatest power of the function is positive, the curve moves away from the $x$x - axis positively.

Thirdly, always check the position of the $y$y - intercept. For example, in the above sketch, at $x=0$x=0, $y=\left(0-1\right)\left(0+1\right)^2\left(0-2\right)^3=8$y=(0−1)(0+1)2(0−2)3=8 and this confirms the direction of the curve downward toward the first positive root.

In all this we need more mathematical tools to determine the positions of local turning points, but the important principles here allow us to understand the functions basic shape.

Worked examples

Question 1

The function $y=x\left(x+3\right)\left(x-2\right)$y=x(x+3)(x−2) has three roots $0,-3$0,−3 and $2$2 all of multiplicity $1$1. It is of degree $3$3 with a $y$y-intercept of $\left(0\right)\left(-3\right)\left(2\right)=0$(0)(−3)(2)=0. The shape is shown as graph $G2$G2 here.

Question 2

The function $y=-\left(x-1\right)\left(x+2\right)^2$y=−(x−1)(x+2)2 has a root of multiplicity $1$1 at $x=1$x=1 and a root of multiplicity $2$2 ($2$2 equal roots) at $x=-2$x=−2. The $y$y - intercept is $-\left(-1\right)\left(2\right)^2=4$−(−1)(2)2=4. The function is of odd degree, so its ends move off in different directions. Note that for large positive values of $x$x, the curve becomes very negative (See graph $G3$G3 below).

Question 3

The function $y=\frac{1}{2}\left(x-3\right)^2\left(x+1\right)^3$y=12​(x−3)2(x+1)3 is of degree $5$5, with a double root at $x=3$x=3 and a triple root at $x=-1$x=−1. The y intercept is $4.5$4.5. The coefficient $\frac{1}{2}$12​ at the front simply halves the size of every $y$y value, but note that there is no change at all in the position of the roots because half of zero is still zero (see graph $G4$G4 below).

 

Practice questions

Question 4

Question 5

Question 6

 

Applications of polynomials

 

Worked examples

Question 7

Brooklyn Bridge is a cable stayed suspension bridge in New York City. Its construction was one of the industrial wonders of the modern world. The curved cable is parabolic and the approximate dimensions of the bridge within the two massive pylons are indicated in the diagram here:

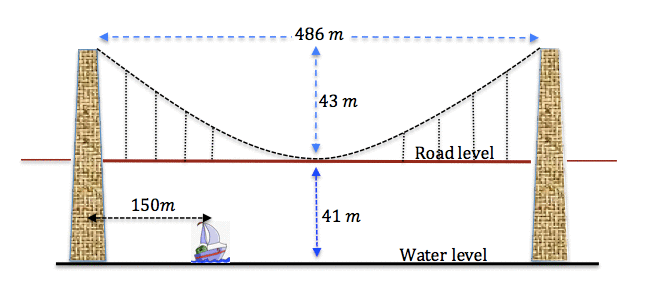
Suppose we have been asked to determine the height above sea-level of the cable at the point directly above a sailing ship that is $150$150 meters in from the left pylon as shown.

Think:  We first need to model the suspension cable with a parabola. To  do this we imagine an $x$x - axis at water level and a $y$y -axis through the least point of the cable, so that we can write coordinates of the least cable point as $\left(0,41\right)$(0,41). 

Our parabola then has the form $y=ax^2+41$y=ax2+41, and we need to determine the leading coefficient $a$a. 

To do this we need another point, and with a little thought, we can ascertain that the coordinate of the point where the cable ties to the top of the right pylon as $\left(243,84\right)$(243,84). This point must satisfy our equation and so:

Do:

$84$84	$=$=	$a\left(243\right)^2+41$a(243)2+41
$59049a$59049a	$=$=	$43$43
$a$a	$=$=	$\frac{43}{59049}$4359049​

Reflect:  The value of $a$a is extremely small (approximately $0.000728$0.000728) which makes sense considering that the length of the bridge is about ten times the height at road level. 

This means that our cable parabola is given by $y=\left(\frac{43}{59049}\right)x^2+41$y=(4359049​)x2+41. 

If the ship is $150$150 m from the left pylon, then based on our coordinate system, the $x$x value of the water level point must be given by $x=-\left(243-150\right)=-97$x=−(243−150)=−97. Thus when we substitute this value into our equation we have:

$y=\left(\frac{43}{59049}\right)\left(-97\right)^2+41=47.852$y=(4359049​)(−97)2+41=47.852

Hence the cable point directly above the ship is approximately $48$48 meters above sea-level.

 

Question 8

A cricket ball is fired vertically upwards by a machine so that at time $t$t seconds the height  $h$h meters is given by $h=-4.9t^2+39.2t$h=−4.9t2+39.2t. Determine its maximum height.

Think:  If we take the common factor $-4.9t$−4.9t out we see that $h=-4.9t\left(t-8\right)$h=−4.9t(t−8).

Do:  We thus know by setting $h=0$h=0, that the time of flight is $8$8 seconds. 

Because a graph of height versus time is an inverted parabola, we know that the maximum height is reached when $t=4$t=4 seconds. 

At $t=4$t=4, $h=-4.9\left(4\right)^2+39.2\left(4\right)=78.4$h=−4.9(4)2+39.2(4)=78.4 meters

 

Question 9

A certain ordered listing of numbers have a sum, up to and including the $n$nth term, given by the formula $S_n=\frac{n}{2}\left(7n-1\right)$Sn​=n2​(7n−1). 

So for example, the list up to the sixth term sums to $S_6=\frac{6}{2}\left(7\times6-1\right)=123$S6​=62​(7×6−1)=123.

We might ask how many numbers in the list must be added together so that the sum becomes $3348$3348?

Think:  We can get a feel for the list by recognizing that $S_1=\frac{1}{2}\left(7\times1-1\right)=3$S1​=12​(7×1−1)=3, and so $3$3 must be the first term of the list.

Do:  With $S_2=\frac{2}{2}\left(7\times2-1\right)=13$S2​=22​(7×2−1)=13 we know therefore that the second term is $10$10, so that $3+10=13$3+10=13. The third term could likewise be revealed as $17$17, and the fourth term $24$24 etc.

The question asks when does $S_n=\frac{n}{2}\left(7n-1\right)=3348$Sn​=n2​(7n−1)=3348? This is a quadratic equation that can be solved as follows:

$\frac{n}{2}\left(7n-1\right)$n2​(7n−1)	$=$=	$3348$3348
$n\left(7n-1\right)$n(7n−1)	$=$=	$6696$6696
$7n^2-n$7n2−n	$=$=	$6696$6696
$7n^2-n-6696$7n2−n−6696	$=$=	$0$0
$\left(7n+216\right)\left(n-31\right)$(7n+216)(n−31)	$=$=	$0$0
$n$n	$=$=	$31,-\frac{216}{7}$31,−2167​

Reflect:  Thus, since $n$n must be positive, $31$31 terms are required so that the sum is $3348$3348.

 

Practice questions

QUESTION 10

QUESTION 11

QUESTION 12