13.05 Volume of composite solids

Composite solids are just a combination of simpler solids in disguise.  

To find the volume of composite solids such as these:

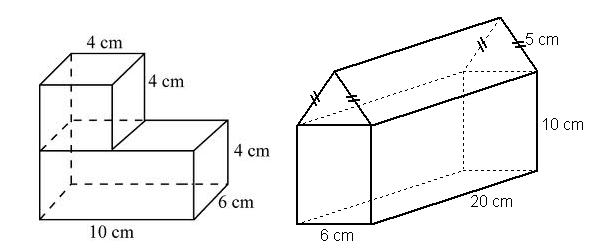
• break down the shape into smaller and simpler solids
• find the volume of the individual smaller solids
• add the volumes of the individual solids to find the total volume

The exception to these steps is when the solid we are looking at is more simply considered as a larger solid with a smaller solid cut out of it, like these ones.

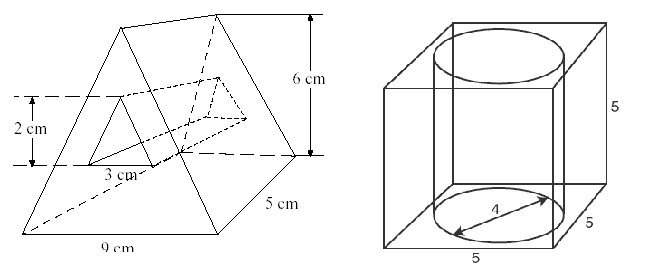
In this case we would

• identify the large solid as well as the solid that has been cut out of it
• find the volume of both pieces
• subtract the volume of the cut-out piece from the volume of the larger piece

We can do this because of the volume addition postulate. In the same way that pieces always add up to the whole for segments, angles, and areas, the same is true for volumes.

Practice questions

Question 1

Question 2

Find the volume of the figure shown, correct to two decimal places.

Reveal SolutionWatch video