4.06 Transformations of quadratics
There are specific names given to different types of polynomials functions. A quadratic function is a polynomial function of degree $2$2, and functions of this form share many of the same properties.
Key characteristics of $y=x^2$y=x2
The most basic type of quadratic function is an equation of the form $y=x^2$y=x2. When graphed, this relation creates a shape that is called a parabola. It is the parent function for all other quadratic functions because all other quadratic functions are transformations of this function. Below is a graph of the function $y=x^2$y=x2. What key characteristics can you identify from the graph?

A graph of the function $y=x^2$y=x2 showing its axis of symmetry and vertex.
By the graph above we can see that the graph of $y=x^2$y=x2 is symmetric across the line $x=0$x=0, or the line of symmetry. It has a minimum turning point at the point $\left(0,0\right)$(0,0). This turning point value is called the vertex. In the case of this graph, the vertex is also the same point as both the $x$x- and $y$y-intercepts.
Transformations of the parent function $y=x^2$y=x2
Let's explore how a quadratic function changes using the applet below. What happens when we change the sliders for dilation, reflection, vertical translation and horizontal translation? Can you describe what changes these values make to the quadratic function?
These movements are called transformations. Transform means change, and these transformations change the simple quadratic $y=x^2$y=x2 into other quadratics by moving (translating), flipping (reflecting) and making the graph appear more or less steep (dilating).
By using the above applet, step through these instructions:
- Start with the simple quadratic $y=x^2$y=x2
- Dilate the quadratic by factor of $2$2
- Reflect on the $x$x-axis
- Translate vertically by $2$2 and horizontally by $-3$−3 units
How has the graph changed? Can you visualize the changes without using the applet? What is the resulting equation?
Equations and transformations of quadratics
Transforming a quadratic will change its equation. Here are some of the most common types of quadratic equations, and what they mean with regards to the transformations that have occurred.
$y=ax^2$y=ax2
If $a<0$a<0 (that is, $a$a is negative) then we have a reflection parallel to the $x$x-axis. It's like the quadratic has been flipped upside down.
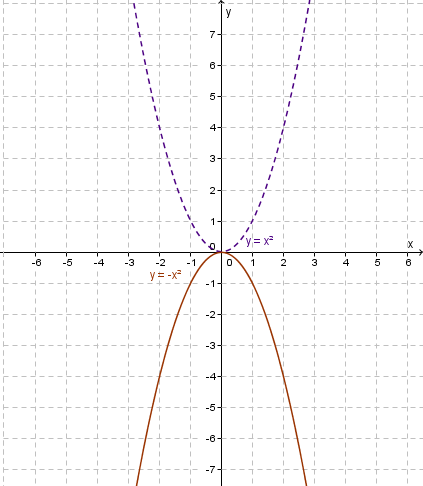
Shows the reflection of
$y=x^2$y=x2 to $y=-x^2$y=−x2
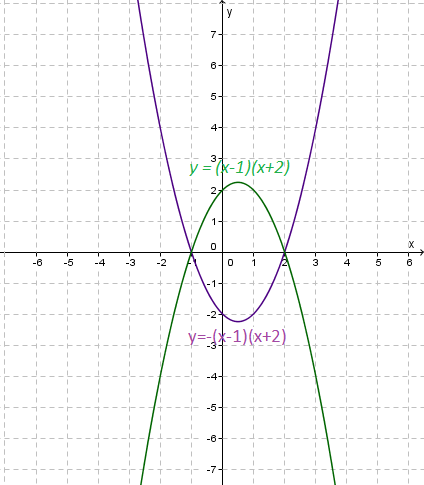
Shows the reflection of
$y=\left(x-1\right)\left(x+2\right)$y=(x−1)(x+2) to $y=-\left(x-1\right)\left(x+2\right)$y=−(x−1)(x+2)
$y=ax^2$y=ax2
This is a quadratic that has been dilated vertically by a factor of $a$a.
If $\left|a\right|>1$|a|>1 then the graph is steeper than $y=x^2$y=x2.
If $\left|a\right|<1$|a|<1 then the graph is flatter than $y=x^2$y=x2.
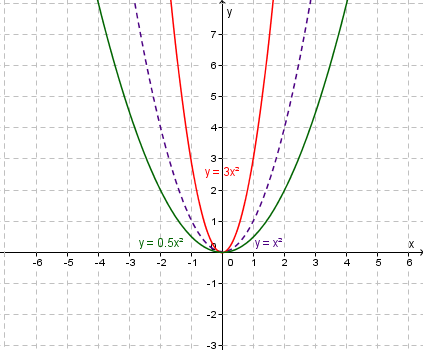
Dilation of $y=x^2$y=x2 to $y=3x^2$y=3x2 and $y=\frac{1}{2}x^2$y=12x2
$y=ax^2+k$y=ax2+k
In the graph $y=ax^2+k$y=ax2+k, the quadratic has been vertically translated by $k$k units.
If $k>0$k>0 then the translation is up.
If $k<0$k<0 then the translation is down.
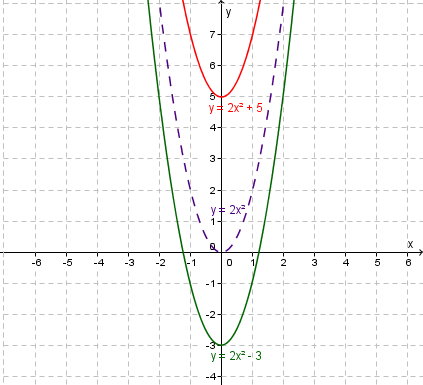
Vertical translation.
Showing one curve $y=2x^2+5$y=2x2+5 having a vertical translation of up $5$5 units, and
another $y=2x^2-3$y=2x2−3 having a vertical translation of down $3$3 units.
$y=\left(x-h\right)^2$y=(x−h)2
The $h$h indicates the horizontal translation.
If $h>0$h>0, that is the factor in the parentheses is $\left(x-h\right)$(x−h) than we have a horizontal translation of $h$h units right.
If $h<0$h<0, that is the factor in the parentheses is $\left(x-\left(-h\right)\right)=\left(x+h\right)$(x−(−h))=(x+h) than we have a horizontal translations of $h$h units left.
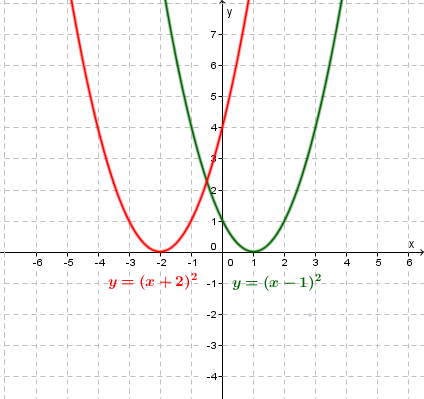
The graph $y=x^2$y=x2 being horizontally translated $2$2 units left
to $y=\left(x+2\right)^2$y=(x+2)2 and $1$1 unit right to $y=\left(x-1\right)^2$y=(x−1)2
The vertex
The vertex (sometimes called turning point) of a quadratic is the point where the function turns. At this point, the function can have a maximum or minimum value.
It changes from being decreasing to increasing, like in this positive quadratic.

Or changes from being increasing to decreasing, like in this negative quadratic.

Vertex form
The form $y=a\left(x-h\right)^2+k$y=a(x−h)2+k is called vertex form. It's really useful for two reasons:
- It tells us the vertex immediately, and knowing the vertex we can draw a pretty good sketch of any quadratic.
- It explains to us a number of transformations that have occurred to the quadratic from the simple quadratic $y=x^2$y=x2.
The form $y=a\left(x-h\right)^2+k$y=a(x−h)2+k shows us:
Vertical dilation $a$a
- If $\left|a\right|>1$|a|>1 then the quadratic is steeper than $x^2$x2.
- If $\left|a\right|<1$|a|<1 then the quadratic is flatter than $x^2$x2.
Reflection $a$a
- If $a<0$a<0 then the quadratic is a reflection of $ax^2$ax2 on a line parallel to the $x$x-axis.
Vertical translation $k$k
- If $k>0$k>0 then the translation is up.
- If $k<0$k<0 then the translation is down.
Horizontal translation $h$h
- If $h<0$h<0 then the translation is to the left, and $x+h$x+h appears in the parentheses.
- If $h>0$h>0 then the translation is to the right, and $x-h$x−h appears in the parentheses.
Practice questions
Question 1
The function $y=-5x^2$y=−5x2 has what dilation factor?
Dilation factor $=$= $\editable{}$
Question 2
The quadratic $y=x^2$y=x2 has been transformed into $y=3\left(x-4\right)^2$y=3(x−4)2. Has there been a reflection?
Yes, across the $x$x-axis
AYes, across the $y$y-axis
BNo$\text{ }$
C
Question 3
The quadratic $y=x^2$y=x2 has been transformed into $y=-4\left(x+10\right)^2$y=−4(x+10)2. Identify the vertical translation.
$0$0 units up or down
A$4$4 units up
B$10$10 units down
C$10$10 units up
D