9.03 Rotations

A rotation occurs when we turn an object or shape around a central point.  On the $xy$xy-plane we usually rotate about the origin, $\left(0,0\right)$(0,0). The preimage and image are congruent, just rotated around (like going in a circle). Every point on the object or shape has a corresponding point on the image.  

Commonly we describe rotations using a degree measure, and as being either clockwise or counterclockwise.

 

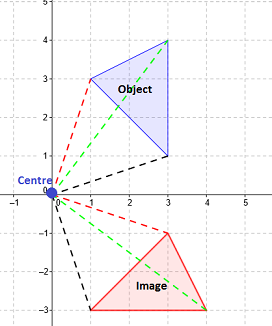
In this example, the image is rotated around the origin by $90^\circ$90° clockwise.  

Note how each point creates a $90^\circ$90° angle with the origin.  

$\left(1,3\right)$(1,3) becomes $\left(3,-1\right)$(3,−1)

$\left(3,1\right)$(3,1) becomes $\left(1,-3\right)$(1,−3)

$\left(3,4\right)$(3,4) becomes $\left(4,-3\right)$(4,−3)

 

Generally speaking we can see that for a rotation of $90^\circ$90° clockwise about the origin, that the $\left(a,b\right)$(a,b) becomes $\left(b,-a\right)$(b,−a). We can also say that this object was transformed by a $270^\circ$270° counterclockwise rotation about the origin.

 

Exploration

Using the applet below you might like to investigate what happens for rotations of $90^\circ$90°, $180^\circ$180°, $270^\circ$270° and $360^\circ$360° in the clockwise direction.

Use the "Alter angle" slider down at the bottom to rotate the image. Click and drag the large blue dot with the arrow to change the center.

What connections can you make to reflections?

How do the coordinates of the vertices change based on the rotation?

 

Practice questions

Question 1

Question 2

Question 3