Investigation: Roller coaster polynomials
Have you ever noticed that the shape of most rollercoasters is similar to the shape of polynomial equations? In this investigation, we will look at different polynomials and the different types of roller coasters they would produce.
Objectives
- To envision polynomials in real life.
- To practice finding zeros of polynomials.
Materials
- Construction paper
- Computer paper
- Crayons
- Pen
- Graphing calculator or graphing application
Before you begin
Work with a friend to answer the following questions:
- What defines a function?
- What is the difference between a function and a relation?
- Would the following roller coaster loop be considered a function? Why or why not?
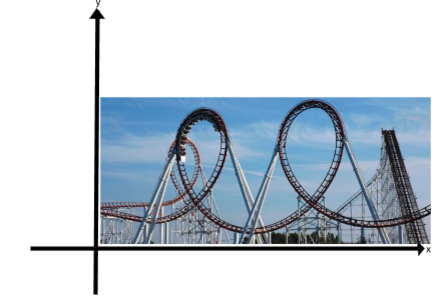
- Based on your answer to question 3 what types of roller coasters can be defined by functions?
Procedure
- Pick coefficients for the boxes in the four following polynomials:
\left(x^{2} + \editable{} x + \editable{}\right) \left( \editable{} x - \editable{}\right)
\left(x - \editable{}\right)^{2} - \left( \editable{} x - \editable{}\right) - \left( \editable{} x^{3} + \editable{}\right)
- x^{8} - \editable{} x^{7} + \editable{} x^{6} - \editable{} x^{5} + \editable{} x^{3} - \editable{} x + \editable{}
\left( \editable{} x - \editable{}\right) \left(x - \editable{}\right) \left(x - \editable{}\right) \left(x - \editable{}\right) \left(x - \editable{}\right)
- Using your graphing calculator or graphing application graph the four equations you have created.
- Draw a sketch of each of these graphs on your piece of computer paper.
Questions for reflection
- Which of the four equations do you think would make the best roller coaster? Answer the following questions based on the roller coaster you have selected.
- Graph the roller coaster you have selected on your piece of construction paper. Only graph the sections of the roller coaster you would build.
- What are the domain and range of the graph you created? Interpret them in terms of the situation.
- For what intervals is your roller coaster increasing?
- For what intervals is your roller coaster decreasing?
- At what interval(s) would the roller coaster be going fastest? Why?
- Is the graph of the roller coaster continuous or discrete?
- How many x-intercepts does the graph have?
- Based on the degree of the polynomial what is the most amount of zeros that the polynomial could have had?
- What are the zeros of this graph? What are the multiplicities of each?
- Where is the graph concave up? What is happening with the roller coaster at this point?
- Where is the graph concave down? What is happening with the roller coaster at this point?
- How many turning points does the polynomial have? What does this mean in the context of the roller coaster scenario?
- Based on the degree of the polynomial what is the most amount of turning points that the polynomial could have had?
Work with a partner
- Can you come up with a polynomial that would produce a roller coaster with 2 peaks?
- Can you come up with a polynomial that would produce a roller coaster with 3 peaks?
- How did you come up with the equations?