We have looked at using integration to find the area between a curve and an axis. Now, we will consider finding the area bounded by multiple curves. There are a number of scenarios to consider and it is useful to remember areas between and under curves can be calculated by using any combination of the following:
- Standard formulas for known geometrical shapes (rectangles, triangles, trapezia)
- Definite integrals
- Subtracting one area from another
Areas between multiple curves and an axis
Sometimes we are required to find the area formed between multiple curves and an axis. The key to solving these problems is finding any points of intersection, dividing the area into sections, then evaluating and summing the integrals associated with each section. Sometimes it is useful to check if standard area formulae can help in obtaining a solution.
Worked examples
Example 1
By drawing the curves $y=2x$y=2x and $y=2(x-2)^2$y=2(x−2)2, find the area bounded by the curves and the $x$x-axis.
Think: This problem involves multiple curves and hence requires drawing the graphs to see what the area looks like.
Do: By drawing both curves and shading the region of interest we get the following.
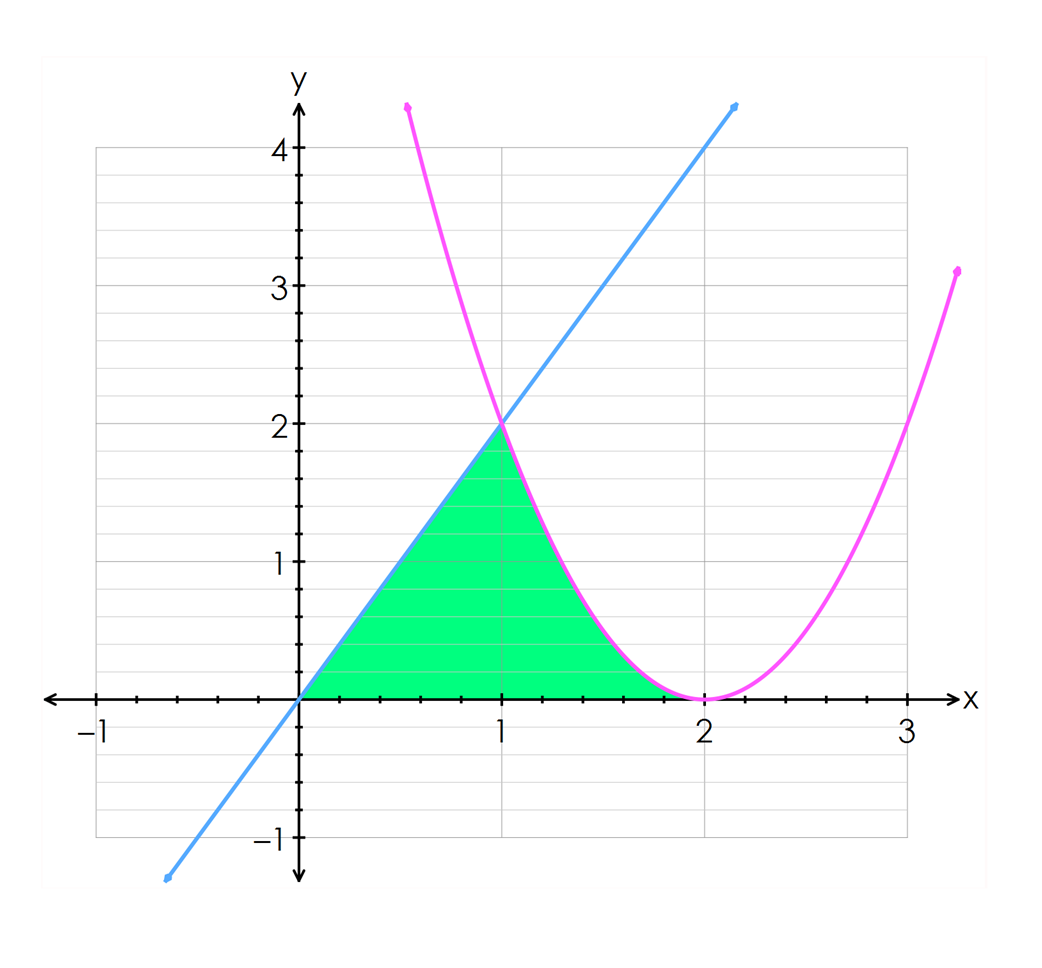
We can see from the graph that there is a point of intersection at $x=1$x=1. We could also determine this by solving the two functions simultaneously.
To calculate this area, we need to divide it up into two sections, each section equivalent to the area underneath the functions. We will calculate the area under the function $y=2x$y=2x between $0$0 and $1$1 and add this to the area under the function $y=2(x-2)^2$y=2(x−2)2 between $1$1 and $2$2. We can setup the following integral to calculate the area, noting that the point of intersection becomes a boundary value of both integrals:
| Area | $=$= | $\int_0^1\ 2x\ dx+\int_1^2\ 2(x-2)^2\ dx$∫10 2x dx+∫21 2(x−2)2 dx |
| Area | $=$= | $[x^2]_0^1+\left[\frac{2\left(x-2\right)^3}{3}\right]_1^2$[x2]10+[2(x−2)33]21 |
| Area | $=$= | $\left[1-0\right]+\left[0-(-\frac{2}{3})\right]$[1−0]+[0−(−23)] |
| Area | $=$= | $1+\frac{2}{3}$1+23 |
| Area | $=$= | $1\frac{2}{3}$123 |
Example 2
Find the area bounded by the curve $y=x^2$y=x2, the $y$y-axis and the lines $y=0$y=0 and $y=4$y=4.
Think: This area is above a curve, not below. However, we can see that we could subtract the area below the curve (the blue area in the diagram below) from the area of the rectangle formed by the $x$x and $y$y-axes and the lines $x=2$x=2 and $y=4$y=4.
Do: We can set up the following equation involving an integral to found the area:
| Area | $=$= | Area of rectangle $-\int_0^2\ x^2\ dx$−∫20 x2 dx |
| Area | $=$= | $(4\times2)-\left[\frac{x^3}{3}\right]_0^2$(4×2)−[x33]20 |
| Area | $=$= | $8-(\frac{8}{3}-\frac{0}{3})$8−(83−03) |
| Area | $=$= | $5\frac{1}{3}$513 units2 |
Practice questions
Question 1
Find the area bounded between the two curves $y=\sqrt{x+5}$y=√x+5 and $y=-x-3$y=−x−3 and the $x$x-axis.
Question 2
Find the exact area between the graph of $y=\sqrt{4-x^2}$y=√4−x2 and the lines $x=2$x=2 and $y=2$y=2.
Areas between two curves
When calculating the area between two curves, we subtract the integral of the bottom curve from the integral of the top curve.
Worked examples
EXAMPLE 3
Find the area enclosed between the curve $y=x^2$y=x2 and the line $y=x+2$y=x+2.
Think: This problem involves multiple curves and hence requires drawing the graphs to see what the area looks like but first we need to find the points of intersection between the two functions.
Do: To find the points of intersection we equate the two functions:
| $x^2$x2 | $=$= | $x+2$x+2 |
| $x^2-x-2$x2−x−2 | $=$= | $0$0 |
| $(x-2)(x+1)$(x−2)(x+1) | $=$= | $0$0 |
| $x$x | $=$= | $2,-1$2,−1 |
Sketching both functions on the same axes and shading the area between them gives:
We can see that the straight line is above the parabola for the given area, therefore we subtract the integral of the parabola from the integral of the straight line as follows:
| Area | $=$= | $\int_{-1}^2\ (x+2)\ dx-\int_{-1}^2\ x^2\ dx$∫2−1 (x+2) dx−∫2−1 x2 dx |
| Area | $=$= | $\int_{-1}^2\ (x+2-x^2)\ dx$∫2−1 (x+2−x2) dx |
| Area | $=$= | $\left[\frac{x^2}{2}+2x-\frac{x^3}{3}\right]_{-1}^2$[x22+2x−x33]2−1 |
| Area | $=$= | $(\frac{2^2}{2}+2(2)-\frac{2^3}{3})-(\frac{(-1)^2}{2}+2(-1)-\frac{(-1)^3}{3})$(222+2(2)−233)−((−1)22+2(−1)−(−1)33) |
| Area | $=$= | $(2+4-\frac{8}{3})-(\frac{1}{2}-2+\frac{1}{3})$(2+4−83)−(12−2+13) |
| Area | $=$= | $4\frac{1}{2}$412 units2 |
Example 4
By drawing the curves $y=6-2x$y=6−2x and $y=x\left(x-3\right)^2$y=x(x−3)2, find the area bounded by the two curves.
Think: Graphing gives us the following two regions trapped between the curves. Notice that on the left the cubic function is uppermost while on the right the linear functions is uppermost.

Do: Because we need the area under the upper curve minus the area under the lower curve at all times, we need to create two calculations to accommodate where the curves switch positions at the intersection point. We'll need to set the integral up in two parts like this:
| Area | $=$= | $\int_1^2\ (x^3-6x^2+9x)-(6-2x)\ dx+\int_2^3\ (6-2x)-(x^3-6x^2+9x)\ dx$∫21 (x3−6x2+9x)−(6−2x) dx+∫32 (6−2x)−(x3−6x2+9x) dx |
| Area | $=$= | $\int_1^2\ (x^3-6x^2+11x-6)\ dx+\int_2^3\ (6-11x+6x^2-x^3)\ dx$∫21 (x3−6x2+11x−6) dx+∫32 (6−11x+6x2−x3) dx |
| Area | $=$= | $\left[\frac{x^4}{4}-2x^3+\frac{11x^2}{2}-6x\right]_1^2+\left[6x-\frac{11x^2}{2}+2x^3-\frac{x^4}{4}\right]_2^3$[x44−2x3+11x22−6x]21+[6x−11x22+2x3−x44]32 |
| Area | $=$= | $(-2+\frac{9}{4})+(\frac{9}{4}-2)$(−2+94)+(94−2) |
| Area | $=$= | $\frac{1}{4}+\frac{1}{4}$14+14 |
| Area | $=$= | $\frac{1}{2}$12 units2 |
Reflect: If we realised that each shaded portion was the same in shape and size (a reflection of each other, or a rotation) we could have calculated one area and then multiplied by $2$2, saving us a lot of time.
Practice questions
Question 3
Consider the functions $y=x^2$y=x2 and $y=x+2$y=x+2.
Graph the functions on the axes below.
Loading Graph...State the values of $x$x at which the line and the parabola intersect.
Write both values on the same line, separated by a comma.
Hence find the area enclosed between the line and the curve.
Question 4
Consider the functions $y=x\left(x-4\right)^2$y=x(x−4)2 and $y=x$y=x.
Graph the functions on the axes below.
Loading Graph...State the values of $x$x at which the line and the curve intersect.
Write all of the values on the same line, separated by commas.
Hence find the area bounded between the line and the curve.

.svg)
.svg)