Definition of a sequence
An ordered collection of numbers or objects is called a sequence or progression. It is similar to a set, but it may contain repetition and its order is important. If the sequence ends, it is known as a finite sequence. Otherwise, it is said to be infinite. For example $−3,5,13,21$−3,5,13,21... and $1,10,100,1000$1,10,100,1000... are examples of mathematical sequences. The "..." at the end of each denotes that these sequences are infinite.
Common difference and the first term
A sequence in which each term changes from the last by adding a constant amount is called an arithmetic sequence. We refer to the constant the terms are changing by as the common difference, which will result from subtracting any two successive terms $\left(T_n-T_{n-1}\right)$(Tn−Tn−1). $T_n$Tn is known as the $n$nth term and $T_{n-1}$Tn−1 is the term directly preceding it.
The first sequence written above $-3,5,13,21,\ldots$−3,5,13,21,… is an arithmetic sequence with a common difference of $8$8. On the other hand, the second sequence $1,10,100,1000,\ldots$1,10,100,1000,… is not arithmetic because the difference between each term is not constant.
The common difference is very important in defining our sequence, but we need one extra piece of information to know exactly what numbers we are dealing with–we need to know where the sequence starts. We denote the first term by the letter $a$a and the common difference by the letter $d$d. We know each term differs from the previous one by $d$d, since, $T_2=T_1+d$T2=T1+d, $T_3=T_2+d$T3=T2+d and so on.
Recurrence relation
A recurrence relation is an equation that defines a sequence based on a rule that gives the next term as a function of the previous term (or terms). So, we can write any arithmetic sequence as the recurrence relation:
$T_n=T_{n-1}+d,T_1=a$Tn=Tn−1+d,T1=a
A recurrence relation is a very straight forward way of describing the sequence, but it isn't very helpful for finding specific terms. For example, if we wanted to find $T_{100}$T100, we would have to list out every single term so that we could get to the point where we find:
$T_{100}=T_{99}+d$T100=T99+d
Explicit formula
We can, in fact, find an explicit formula written solely in terms of $a$a and $d$d. This is useful for finding the $n$nth term without listing the sequence in full.
Let's look at a table of a concrete example to see the pattern for the explicit formula. Returning to the sequence $-3,5,13,21,\ldots$−3,5,13,21,…, we have $a=-3$a=−3 and $d=8$d=8.
| $n$n | $T_n$Tn | Pattern |
|---|---|---|
| $1$1 | $-3$−3 | $-3$−3 |
| $2$2 | $5$5 | $-3+8$−3+8 |
| $3$3 | $13$13 | $-3+2\times8$−3+2×8 |
| $4$4 | $21$21 | $-3+3\times8$−3+3×8 |
| ... | ||
| $n$n | $T_n$Tn | $-3+(n-1)\times8$−3+(n−1)×8 |
The pattern starts to become clear and we could guess that the tenth term becomes:
$T_{10}=69=-3+9\times8$T10=69=−3+9×8
And the one-hundredth term:
$T_{100}=789=-3+99\times8$T100=789=−3+99×8
And following the pattern, the explicit formula for the $n$nth term is:
$T_n=-3+(n-1)\times8$Tn=−3+(n−1)×8
We could create a similar table for an arithmetic progression with starting value $a$a and common difference $d$d and we would observe the same pattern. Hence, the general rule for finding the the $n$nth term of any arithmetic sequence is given by:
$T_n=a+\left(n-1\right)d$Tn=a+(n−1)d
For any arithmetic sequence with starting value $a$a and common difference $d$d, we can express the $n$nth term in either of the following two forms:
- Recursive form is a way to express any term in relation to the previous term:
$T_n=T_{n-1}+d$Tn=Tn−1+d, where $T_1=a$T1=a
- Explicit form is a way to express any term in relation to the term number:
$T_n=a+\left(n-1\right)d$Tn=a+(n−1)d
Remember, an arithmetic sequence is defined by the presence of a common difference, that is, $d=T_n-T_{n-1}$d=Tn−Tn−1. In practice, we confirm this by using any $3$3 consecutive terms, for example, $T_2-T_1=T_3-T_2$T2−T1=T3−T2.
Worked examples
Example 1
For the sequence $87,80,73,66...$87,80,73,66..., find an explicit rule for the $n$nth term and hence, find the $30$30th term.
Think: Check that the sequence is arithmetic, does each term differ from the last by a constant? Then write down the starting value $a$a and common difference $d$d and substitute these into the general form: $T_n=a+(n-1)d$Tn=a+(n−1)d
Do: Each term decreases from the last by $7$7. So we have an arithmetic sequence with: $a=87$a=87 and $d=-7$d=−7. The general formula for this sequence is:
$T_n=87+\left(n-1\right)\times\left(-7\right)$Tn=87+(n−1)×(−7) or $T_n=87-7(n-1)$Tn=87−7(n−1)
Hence, the $30$30th term is:
$T_{30}=87-7\times29=-116$T30=87−7×29=−116
Example 2
If an arithmetic sequence has $T_5=38$T5=38 and $T_9=66$T9=66, find the recurrence relation for the sequence.
Think: To find the recurrence relation we need the starting value and common difference. As we have two terms we can set up two equations in terms of $a$a and $d$d using $T_n=a+(n-1)d$Tn=a+(n−1)d, which applies to any term of an arithmetic sequence.
Do:
| $T_5$T5: | $a+4d=38$a+4d=38 | $.....\left(1\right)$.....(1) |
and
| $T_9$T9: | $a+8d=66$a+8d=66 | $.....\left(2\right)$.....(2) |
If we now subtract equation $\left(1\right)$(1) from equation $\left(2\right)$(2) the first term in each equation will cancel out to leave us with:
| $\left(8d-4d\right)$(8d−4d) | $=$= | $66-38$66−38 |
| $4d$4d | $=$= | $28$28 |
| $\therefore d$∴d | $=$= | $7$7 |
With the common difference found to be $7$7, we can substitute this back into the equation $\left(1\right)$(1) $a+4\times7=38$a+4×7=38 and find that $a$a is $10$10. The recurrence relation for this sequence is given by:
$T_n=T_{n-1}+7,T_1=10$Tn=Tn−1+7,T1=10
Not all recursive forms define an arithmetic sequence.
For example, a sequence is given recursively as $T_{\left(n+1\right)}=T_n+n$T(n+1)=Tn+n, with $T_1=0$T1=0. On first look, this seems like the other sequences we have seen today. To test whether it is an arithmetic sequence, we will consider the first four terms. Here:
$T_1=0,T_2=T_1+2=2,T_3=T_2+3=2+3=5,T_4=T_3+4=5+4=9$T1=0,T2=T1+2=2,T3=T2+3=2+3=5,T4=T3+4=5+4=9
The difference in successive terms is not constant but rise by $1$1 each time. So while there is definitely a pattern to the sequence, it is not arithmetic.
Arithmetic sequences in tables and graphs
For any arithmetic sequence in the general form given by $T_n=a+\left(n-1\right)d$Tn=a+(n−1)d, we can expand the bracket and collect like terms, creating a simplified generating rule of the form $T_n=dn+k$Tn=dn+k where $d$d and $k$k are constants.
For example, the rule $T_n=5+\left(n-1\right)\times2$Tn=5+(n−1)×2 is equivalent to $T_n=2n+3$Tn=2n+3. This is in the form of the equation of a straight line $\left(y=mx+c\right)$(y=mx+c). If an arithmetic sequence is plotted as a series of points, they will all lie on a straight line with the gradient being the common difference. This makes sense since we have a constant rate of change in all arithmetic sequences.
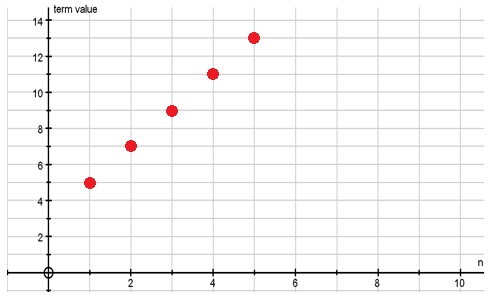
The first term is represented by the point shown at $n=1$n=1, $T_1=5$T1=5 and we can see the gradient here is the common difference $d=2$d=2.
We could also be expected to recognise an arithmetic sequence from a table, such as:
| $n$n | $1$1 | $2$2 | $3$3 | $4$4 | $5$5 |
|---|---|---|---|---|---|
| $T_n$Tn | $5$5 | $7$7 | $9$9 | $11$11 | $13$13 |
Here, we can read off the initial term $T_1=5$T1=5 and the common difference can be seen in step between the $T_n$Tn values in the second row.
Use the following applet to explore the features of a graph that represents an arithmetic sequence.
|
|
Applications of arithmetic sequences
Arithmetic sequences grow linearly, literally meaning ‘in a straight line’. We find applications of linear growth in many areas of life, including simple interest earnings, straight-line depreciation, monthly rental accumulation and many others. For example, if you are saving money in equal instalments the cumulative savings at each savings period form an arithmetic sequence. If you are travelling down a highway at a constant speed then the amount of petrol left in the tank, if measured every minute of the trip, forms another arithmetic progression. Whenever something grows or diminishes in constant quantities over equal time periods then that growth or decline is said to be linear.
Worked example
Example 3
Tabitha starts with $\$200$$200 in her piggy bank, the following week she adds $\$25$$25 and then continues to add $\$25$$25 at the start of each successive week. Find a rule to describe $B_n$Bn the balance of her savings at the start of the $n$nth week and find when her savings will reach $\$450$$450.
Think: The sequence of savings generated is $\$200,\$225,\$250,\$275...$$200,$225,$250,$275... This is arithmetic, so write down the starting value and common difference and use $T_n=a+\left(n-1\right)d$Tn=a+(n−1)d to find a general rule.
Do: $a=200$a=200 and $d=25$d=25 and so our general rule is: $B_n=200+25(n-1)$Bn=200+25(n−1) or equivalently $B_n=175+25n$Bn=175+25n.
To find when the savings reach $\$450$$450, we substitute this into our general rule and solve for $n$n:
| $450$450 | $=$= | $175+25n$175+25n |
| $\therefore25n$∴25n | $=$= | $275$275 |
| $n$n | $=$= | $11$11 |
Hence, at the start of the $11$11th week her savings will have grown to $\$450$$450.
Practice questions
Question 1
The $n$nth term in an arithmetic sequence is given by the formula $T_n=14+5\left(n-1\right)$Tn=14+5(n−1).
Determine $a$a, the first term in the arithmetic sequence.
Determine $d$d, the common difference.
Determine $T_{10}$T10, the $10$10th term in the sequence.
Question 2
The plotted points represent terms in an arithmetic sequence:
Complete the table of values for the given points.
$n$n $1$1 $2$2 $3$3 $4$4 $T_n$Tn $\editable{}$ $\editable{}$ $\editable{}$ $\editable{}$ Identify $d$d, the common difference between consecutive terms.
Write a simplified expression for the general $n$nth term of the sequence, $T_n$Tn.
Find the $15$15th term of the sequence.
Question 3
Zuber is a taxi service that charges a $\$1.50$$1.50 pick-up fee and $\$1.95$$1.95 per kilometre of travel.
What is the total charge for a $10$10 km journey?
We want to describe this situation as a recursive sequence.
To start with, state the initial condition $T_0$T0.
Write a recurrence relation for $T_n$Tn in terms of $T_{n-1}$Tn−1 which defines the price of a $n$n km trip.
Question 4
A car bought at the beginning of 2009 is worth $\$1500$$1500 at the beginning of 2015. The value of the car has depreciated by a constant amount of $\$50$$50 each year since it was purchased.
What was the car purchased for in 2009?
Plot the value of the car, $V_n$Vn, on the graph from 2009 (represented by $n=0$n=0) to 2015 (represented by $n=6$n=6).
Loading Graph...Write an explicit rule for the value of the car after $n$n years.
Give the rule in its expanded form.
Solve for the year $n$n at the end of which the car will be worth half the price it was bought for.