Topics
6. Similar Figures and Scale factors
topic badge
AustraliaWA
Year 11

6.02 Scale factors in similar figures

Lesson
Worksheet
Practice
Lesson

Similar figures

Recall from our previous lesson that two shapes, or figures, are said to be similar if they are the same shape but different sizes. Two key features of similar figures are:

  • Corresponding angles are equal
  • Corresponding sides are proportional, meaning they have been multiplied by the same scale factor.

Similar shapes are either enlargements or reductions of one another.

The two polygons in this interactive tool are similar. We can look at their relative sizes with different scale factors.

Created with Geogebra

 

Enlargements

A shape is considered an enlargement of another if one shape has side lengths that are all increased by the same scale factor.  

Example

Take a triangle with side lengths measuring $3$3 cm, $4$4 cm and $5$5 cm. If each side is multiplied by the same factor, say $2$2, the new resulting triangle will have side lengths measuring $6$6 cm, $8$8 cm and $10$10 cm. The resulting shape is larger.

 

Reductions

A shape is considered a reduction of another if one shape has side lengths that are all decreased by the same scale factor.  

Consider the reverse of the above example: a triangle with side lengths measuring $6$6 cm, $8$8 cm and $10$10 cm has each side multiplied by a factor of $\frac{1}{2}$12​. The new resulting triangle will have side lengths measuring $3$3 cm, $4$4 cm and $5$5 cm. The resulting shape is smaller than the original.

 

Scale factor

The scale factor tells us by how much the object has been enlarged or reduced.

If the scale factor is greater than $1$1, the image is being made bigger than the original.

If the scale factor is smaller than $1$1, the image is being made smaller than the original. 

 

Worked example

Example 1

The shape $ABCD$ABCD has been transformed to $A'B'C'D'$A′B′C′D′. 

a) Are the two shapes similar?

 

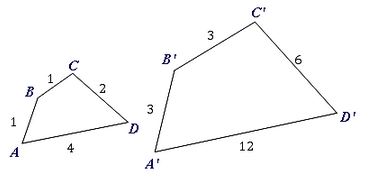
Think: To check if two shapes are similar each pair of corresponding sides must be in the same proportion. Identify corresponding sides, in some cases this might mean rotating or reflecting the shape, and compare the ratios of the matching sides.

Do:

Side Length Side Length Scale factor
$AD$AD $4$4 $A'D'$A′D′ $12$12 $12\div4=3$12÷​4=3
$DC$DC $2$2 $D'C'$D′C′ $6$6 $6\div2=3$6÷​2=3
$CB$CB $1$1 $C'B'$C′B′ $3$3 $3\div1=3$3÷​1=3
$BA$BA $1$1 $B'A'$B′A′ $3$3 $3\div1=3$3÷​1=3

Since all the ratios are the same, we can conclude that $ABCD$ABCD is similar to $A'B'C'D'$A′B′C′D′.

b) What is the scale factor to transform $ABCD$ABCD to $A'B'C'D'$A′B′C′D′?

Think: As we know the shapes are similar we can use the ratio of any two corresponding sides.

Do: The scale factor is $3$3. That is the shape $ABCD$ABCD has been enlarged by a factor of $3$3. 

 

Practice questions

Question 1

The dimensions of the triangle shown are enlarged using a scale factor of $3.1$3.1.

A triangle labeled ABC. Each side of the triangle is labeled with its respective length: side AB measures $23$23 $cm$cm, side BC measures $22$22 $cm$cm, and side AC measures $19$19 $cm$cm. The triangle does not show any angle measurements.

 

  1. What would be the new length of $AB$AB?

  2. What would be the new length of $BC$BC?

  3. What would be the new length of $CA$CA?

Question 2

The two figures to the right are similar.

Two triangles are illustrated. The larger triangle which is on the left side is named as $\triangle ABC$△ABC. The smaller triangle, on the left side, is named as $\triangle PRQ$△PRQ. Each of the triangle has pair of sides that have given measures. In $\triangle ABC$△ABC, the measure of side $AC$AC is $28$28 units and the measure of side $AB$AB is $14$14 units. In $\triangle PRQ$△PRQ, the measure of side $PR$PR is $8$8 units and the measure of side $PQ$PQ is $m$m units. Also, in the illustration, $\angle BAC$∠BAC and $\angle QPR$∠QPR have the same single mark indicating that their measures are congruent. While $\angle ABC$∠ABC and $\angle PQR$∠PQR have the same two angle marks indicating that their measures are also congruent.

 

  1. Find the reduction factor. State your answer as a fraction.

  2. Hence find the value of $m$m.

Question 3

Identify if quadrilateral $A'B'C'D'$A′B′C′D′ is a dilation of quadrilateral $ABCD$ABCD.

Loading Graph...

A Cartesian coordinate plane is marked from -10 to 10 on both $x$x- and $y$y- axes. Quadrilateral A'B'C'D' is smaller and is graphed with vertices A' $\left(-4,2\right)$(−4,2), B' $\left(5,2\right)$(5,2), C' $\left(5,-3\right)$(5,−3), and D' $\left(-4,-3\right)$(−4,−3). Quadrilateral ABCD is bigger and is  graphed with vertices A $\left(-9,4\right)$(−9,4), B $\left(10,4\right)$(10,4), C $\left(10,-6\right)$(10,−6), and D $\left(-9,-6\right)$(−9,−6). (Please refrain from using the distance formula as a hint and encourage them to count the units between the vertices instead. Avoid mentioning the contents within these parentheses regardless of any inquiries from the students.)

  1. yes

    A

    no

    B

 

Problem solving using similar triangles

The sides lengths of similar triangles are in the same ratio or proportion. So once we know that two triangles are similar, by using the properties from our previous lesson, we can find any unknown side lengths by using the ratio. 

To reduce the number of steps required in problem solving start with the unknown in the numerator. For example, when solving for $y$y in the following diagram we can equate the ratio of the corresponding sides from the large triangle to the small triangle: $\frac{y}{10}=\frac{7}{4}$y10​=74​. Alternatively, we can equate the ratio of the sides within the large triangle to the corresponding ratio of sides within the smaller triangle $\frac{y}{7}=\frac{10}{4}$y7​=104​. With either set-up we can solve for $y$y in one step by multiplying both sides by the denominator of the left-hand side.


Practice questions

Question 4

A stick of height $1.1$1.1 m casts a shadow of length $2.2$2.2 m. At the same time, a tree casts a shadow of $6.2$6.2 m.

The tree that has $h$hm height casts a shadow of $6.2$6.2m long. At the same time, a stick with $1.1$1.1m height casts a shadow of $2.2$2.2m long. When connecting the top of the tree to the tip of its shadow, it forms a right triangle. Also, when connecting the tip of the stick to the tip of its shadow, it forms a right triangle. These two triangles formed are similar due to the side that is represented by the heights of stick and tree correspond to each other. Sides representing the lengths of their shadows are corresponding sides.

 

  1. If the tree has a height of $h$h metres, solve for $h$h.

Question 5

 

Outcomes

1.3.6

use the scale factor for two similar figures to solve linear scaling problems

What is Mathspace

About Mathspace