Problem solving strategy
So far in this chapter you have learnt about the various rules and processes associated with trigonometry for all types of triangles. They have allowed us to find unknown sides and angles. We will now apply this knowledge and understanding to various practical applications. Often the biggest challenge is choosing the right solution strategy. Applying the following thought process can be helpful in attaining a correct solution:
- Is a diagram provided? If not, create one with all given information including what you are asked to calculate.
- What type of triangle/s are present in the diagram? Right-angled/Non-right-angled?
- For problems involving right-angled triangles:
- If you are only finding sides of a triangle with no angles involved, use Pythagoras' theorem
- If you are finding angles or using angles to find sides, use right-angled trigonometry (SOHCAHTOA).
- For problems involving non-right-angled triangles use the sine, cosine and area sine rules, (being careful of the ambiguous case of the sine rule).
- Two dimensional applications of trigonometry can involve seemingly difficult concepts but be tackled by using careful, deliberate steps, and a combination of the tools mentioned above.
Right-angled triangle relationships
For any right-angled triangle:

Pythagoras' theorem states: $a^2+b^2=c^2$a2+b2=c2
where $c$c represents the length of the triangle's hypotenuse and $a$a and $b$b are the lengths of the two other sides.
The trigonometric ratios are:
$\sin\theta$sinθ = $\frac{Opposite}{Hypotenuse}$OppositeHypotenuse = $\frac{b}{c}$bc
$\cos\theta$cosθ = $\frac{Adjacent}{Hypotenuse}$AdjacentHypotenuse = $\frac{a}{c}$ac
$\tan\theta$tanθ = $\frac{Opposite}{Adjacent}$OppositeAdjacent = $\frac{b}{a}$ba
The mnemonic SOHCAHTOA can be useful to help remember the ratios.
Exact value triangles:
Non-right-angled triangle relationships
For any non-right-angled triangle with sides $a$a, $b$b, and $c$c, with corresponding opposite angles $A$A, $B$B, and $C$C:

The sine rule states:
$\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}$sinAa=sinBb=sinCc
The cosine rule states:
$c^2=a^2+b^2-2ab\cos C$c2=a2+b2−2abcosC.
The area sine rule states:
$Area=\frac{1}{2}ab\sin C$Area=12absinC
Use the Sine Rule
- When two angles and a side are known and you wish to find the other side
- When two sides and an angle are known and you wish to find the other angle
Use the Cosine Rule
- When you want to find the third side of a triangle when you know two sides and the angle between them
- When you want to find the angles of a triangle when you know all three sides
Angles of elevation and depression
An angle of elevation is the angle created when an observer is looking at a object which is above the horizontal. The angle between the horizontal and the observer's line of sight is called angle of elevation.
An angle of depression is the angle created when an observer is looking at an object which is below the horizontal. The angle between the horizontal and the observer's line of sight is called angle of depression.
Using the angle of elevation or depression, we can create right-angled triangles. If we know the height above or below we can find the distance an object is from an observer, or vice-versa.
Worked examples
Example 1
Calculate the height of the tree below assuming it is vertical and the angle of elevation is $38$38 degrees.

The distance from the base of the tree to a point of observation was $4.2$4.2 m.
The angle of elevation from this point to the top of the tree is $38$38 degrees.
Drawing a right-angled triangle for the given information letting the height of the tree equal $h$h m.

| $\tan38^\circ$tan38° | $=$= | $\frac{\text{height of tree }}{4.2}$height of tree 4.2 m |
| $\text{height of tree }$height of tree | $=$= | $4.2\times\tan38^\circ$4.2×tan38° |
| $\text{height of tree }$height of tree | $=$= | $3.28$3.28 |
So the height of this tree is $3.28$3.28 m.
Practice questions
Question 1
Considering the diagram below, find $x$x, the angle of depression from point $B$B to point $C$C.
Round your answer to two decimal places.

Question 2
A man standing at point $C$C, is looking at the top of a tree at point $A$A. Identify the angle of elevation in the figure given.

A right triangle is shown with vertices labeled A, B and C. Side AB is the vertical leg, side BC is the horizontal leg, and side AC is the hypotenuse. The right angle is at vertex B, as indicated by a small square. There are two arcs indicating angles: one at vertex C, labeled with $\alpha$α, and another at vertex A, labeled with $\theta$θ. Above vertex C, a vertical dotted line extends from vertex C to a point labeled D. The angle between this dotted line CD and the hypotenuse AC is labeled with $\sigma$σ.
$\alpha$α
A$\theta$θ
B$\sigma$σ
C
Question 3
At a certain time of the day a light post, $6$6 m tall, has a shadow of $8.5$8.5 m. If the angle of elevation of the sun at that time is $\theta$θ, find $\theta$θ to the nearest minute.
Question 4
From the top of a rocky ledge $188$188 m high, the angle of depression to a boat is $13^\circ$13°. If the boat is $d$d m from the foot of the cliff find $d$d correct to two decimal places.
Bearings
In surveying and navigation, bearings are used to help identify the location of an object.
The four main directions of a compass are north (N), east (E), south (S) and west (W).

Three-figure (true) bearings
Three-figure bearing are:
- Measured from north ($N$N)
- Measured in a clockwise direction
- Written using three figures
A $T$T is often but not always used to indicate a true bearing. If the angle measure is less than $100^\circ$100° it would be written 040° or 040°T.
To use true bearing to describe the location of a plane at point $B$B from the airport at point $A$A :
- Place the centre of a compass on the starting point, in the case the airport.
- Starting at North, rotate clockwise until we get to the line $AB$AB.
- Write angle as the true bearing of point $B$B.

The true bearing of $B$B from $A$A is $127^\circ$127° or $127^\circ$127°$T$T.
The diagram below describes the bearing of $P$P from $O$O. Rotating clockwise from North, we get an angle of $55^\circ$55°.

Since this measure is less than three digits, we put a 0 in front of it so the true bearing of $P$P is 055°. Consider the true bearing of $O$O from $P$P . Since we are always measuring from north and we are starting at $P$P the true bearing would be $180+55=235^\circ$180+55=235°.
Compass bearings
A compass bearing describes the location of a point using:
- The starting direction of either north or south;
- The acute angle needed to rotate
- The direction to rotate, east or west.
To describe the position of point $B$B from $A$A we would say:
"Starting at South, I then rotate $53$53° towards East."
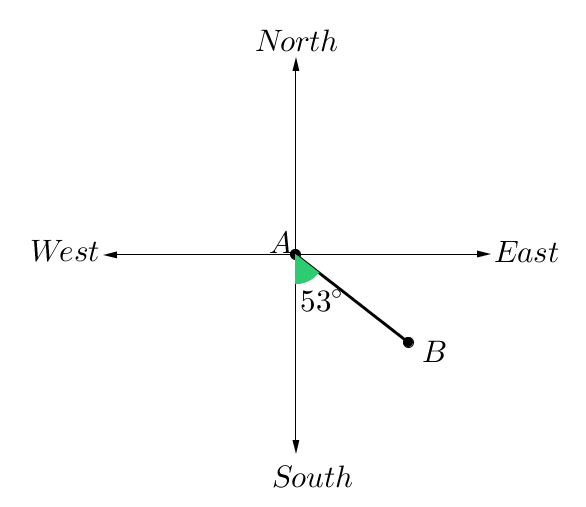
We can write this mathematically as:
$S$S$53$53°$E$E
Which one first?
The bearing needed or used completely depends on which position comes first. Have a look at the investigation below, it quickly shows you how the angle changes depending on if we are measuring the bearing of A from B or B from A.
Worked examples
Example 2
Find the three-figure and the compass bearings of point $P$P from $O$O.
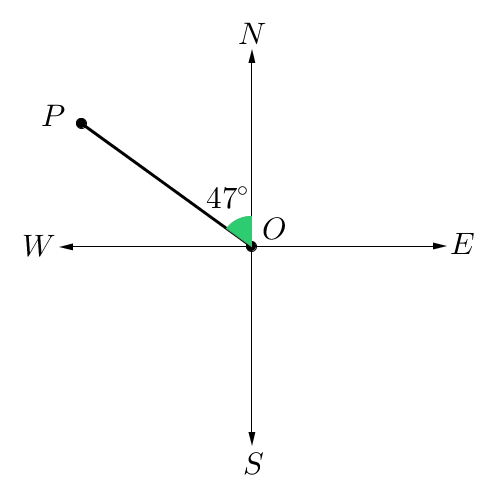
Three-figure bearing:
Starting at North rotate in a clockwise direction.
$360^\circ-47^\circ=313^\circ$360°−47°=313°
The three-figure bearing of $P$P from $O$O is $313^\circ$313°$T$T.
Compass Bearing
Point $P$P is closest to North, so starting at North, rotate $47^\circ$47° towards West.
The compass bearing of $P$P from $O$O is $N$N$47^\circ$47°$W$W.
Example 3

A slightly lost hiker walks $300$300 m east before turning south and walking another $800$800 m. What is its true bearing from its original position (to $1$1 decimal place)? And then what is this as a compass bearing?
Think: Drawing a diagram showing all the information provided is a great way to start. Don't forget, you are trying to create a right-angled or non-right-angled triangle.
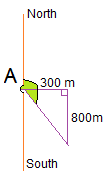
The angle we want to find is in green. It is equal to 90° + the angle inside the triangle that I can find using trigonometry.
Do: Bearing is
| $90+\tan^{-1}\frac{800}{300}$90+tan−1800300 | $=$= | $90+\tan^{-1}\frac{8}{3}$90+tan−183 |
| $=$= | $90+69.44$90+69.44 | |
| $=$= | $159.44$159.44 |
and to 1 decimal place the final bearing is $159.4$159.4°N
As a compass bearing we need to know the acute angle with the North South line. This is $180-159.4=20.6$180−159.4=20.6
The compass points we will use will be South first, and then East, so the compass bearing is S$20.6$20.6°E
Practice questions
Question 5
Consider the point $A$A.

Find the true bearing of $A$A from $O$O.
What is the compass bearing of point $A$A from $O$O?
$\editable{}$ $\editable{}$$^\circ$° $\editable{}$
Question 6
What is the true bearing of Southwest?
Question 7
In the figure below, point $B$B is due East of point $A$A. We want to find the position of point $A$A relative to point $C$C.

Find the true bearing of point $A$A from point $C$C.
What is the compass bearing of point $A$A from point $C$C?
$\editable{}$ $\editable{}$$^\circ$° $\editable{}$
Question 8
The position of a ship S is given to be $20$20 kilometres from P, on a true bearing of $0$0$49$49$^\circ$°T.
The position of the ship can also be given by its $\left(x,y\right)$(x,y) coordinates.

If the ship's $x$x-coordinate is $x$x, find $x$x to one decimal place.
If the ship's y-coordinate is $y$y, find $y$y to one decimal place.
Question 9
Mae observes a tower at an angle of elevation of $12^\circ$12°. The tower is perpendicular to the ground.
Walking $67$67 m towards the tower, she finds that the angle of elevation increases to $35^\circ$35°.

Calculate the angle $\angle ADB$∠ADB.
Find the length of the side $a$a.
Round your answer to two decimal places.
Using the rounded value of the previous part, evaluate the height $h$h, of the tower.
Round your answer to one decimal place.
Question 10
A drone travels due east for $2.2$2.2 km and then travels on a bearing of $S$S$32^{\circ}E$32∘E for $5.9$5.9 km.
We are going to determine the compass bearing needed to return to the starting point.

If the angle of the compass bearing is $a^{\circ}$a∘, what is the form of the compass bearing needed to return to the starting point?
$S\text{ }a^\circ\text{ }W$S a° W
A$S\text{ }a^\circ\text{ }E$S a° E
B$N\text{ }a^\circ\text{ }W$N a° W
C$N\text{ }a^\circ\text{ }E$N a° E
DFind $x$x, the distance between the end point to the start point of the drone's flight.
Express your answer to the nearest two decimal places.
In part (a) we found that the compass bearing needed to return to the starting point is of the form $N$N$a°$a°$W$W. Find $a$a to the nearest degree.
Note that $a=y+z$a=y+z as shown in the diagram.



