Quadratic functions take the shape of a parabola. Parabolas are utilised in bridges, radio telescopes, and car headlights, among other applications, due to their special shape properties. In fact, many famous landmarks are parabolas - for example, the Sydney Harbour Bridge.

The Sydney Harbour Bridge, which is roughly parabolic in shape
Identifying key features
Quadratic functions can be written in any of the following forms:
General Form: $y=ax^2+bx+c$y=ax2+bx+c
Factored or $x$x-intercept form: $y=a\left(x-\alpha\right)\left(x-\beta\right)$y=a(x−α)(x−β)
Turning point form: $y=a\left(x-h\right)^2+k$y=a(x−h)2+k
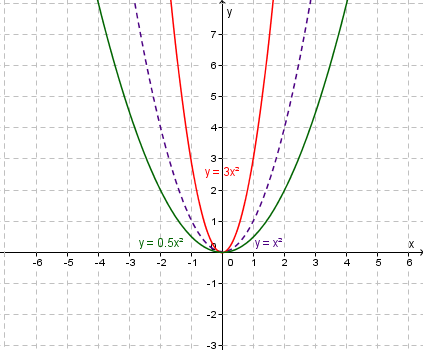
Each form has an advantage for different key features that can be identified quickly. However, for each form the role of $a$a remains the same.
That is:
- If $a<0$a<0 then the quadratic is concave down
- If $a>0$a>0 then the quadratic is concave up
- The larger the magnitude of $a$a, the narrower the curve


Intercepts
The $x$x-intercepts are where the parabola crosses the $x$x-axis. This occurs when $y=0$y=0.
The $y$y-intercept is where the parabola crosses the $y$y-axis. This occurs when $x=0$x=0.
Parabolas can have none, one, or two $x$x-intercepts as shown below.
 |
 |
 |
| No solutions | One solution | Two solutions |
Maximum and minimum values
Maximum or minimum values are also known as the turning points, and they are found at the vertex of the parabola.
 |
 |
|
Parabolas that are concave up have a minimum value. This means the $y$y-value will never go under a certain value. |
Parabolas that are concave down have a maximum value. This means the $y$y-value will never go over a certain value. |
Axis of symmetry
Maximum and minimum values occur on a parabola's axis of symmetry. This is the vertical line that evenly divides a parabola. We can use this symmetry to find the $x$x-value of the vertex by averaging the two $x$x-intercepts (if they exist). Alternatively, we can find the equation of the axis of symmetry and hence the $x$x coordinate of the vertex by using the general form of the quadratic $y=ax^2+bx+c$y=ax2+bx+c and substituting the relevant values of $a$a and $b$b into:
$x=\frac{-b}{2a}$x=−b2a
Graphs of quadratics
Graphs from general form
$y=ax^2+bx+c$y=ax2+bx+c
- From this form we can read the $y$y-intercept directly: $(0,c)$(0,c)
- Find the axis of symmetry using the formula: $x=\frac{-b}{2a}$x=−b2a
- The axis of symmetry is also the $x$x-coordinate of the turning point. Substitute this value into the equation the find the $y$y-coordinate of the turning point
- The $x$x-intercept can be found by substituting $y=0$y=0 into the equation and then using one of our methods for solving quadratics, such as factorising or the quadratic formula, to find the zeros of the equation
Graphs from factored form
$y=a\left(x-\alpha\right)\left(x-\beta\right)$y=a(x−α)(x−β)
- From this form we can read the $x$x-intercepts directly: $(\alpha,0)$(α,0) and $(\beta,0)$(β,0). Since, if $y=0$y=0 we can solve the equation using the null factor law
- The axis of symmetry will be at the $x$x-coordinate midway between the two $x$x-intercepts. Alternatively you could expand this equation to general form and then use the formula for the axis of symmetry: $x=\frac{-b}{2a}$x=−b2a
- The axis of symmetry is also the $x$x-coordinate of the turning point. Substitute this value into the equation the find the $y$y-coordinate of the turning point
- The $y$y-intercept can be found by substituting $x=0$x=0 into the equation
Graphs from turning point form
$y=a\left(x-h\right)^2+k$y=a(x−h)2+k
- This form is given this name as we can read the turning point directly from the equation: $(h,k)$(h,k)
- We can obtain this form by starting with the general form and completing the square
- We can obtain this graph from the graph of $y=x^2$y=x2, by dilating (stretching) the graph by a factor of $a$a from the $x$x-axis, then translating the graph $h$h units horizontally and $k$k units vertically
- The axis of symmetry will be at $x=h$x=h
- The $y$y-intercept can be found by substituting $x=0$x=0 into the equation
- The $x$x-intercept can be found by substituting $y=0$y=0 into the equation and rearranging
Practice questions
Question 1
Consider the quadratic function $y=-x^2+4x+12$y=−x2+4x+12.
What is the concavity of the parabola?
Concave up
AConcave down
BWhat is the $y$y value of the $y$y-intercept?
Find the $x$x values of the $x$x-intercepts.
Find the equation of the axis of symmetry.
Find the coordinates of the vertex of the parabola.
Vertex $=$=$\left(\editable{},\editable{}\right)$(,)
Graph the function $y=-x^2+4x+12$y=−x2+4x+12.
Loading Graph...
Question 2
Consider the parabola $y=\left(x+1\right)\left(x-3\right)$y=(x+1)(x−3).
Find the $y$y value of the $y$y-intercept.
Find the $x$x values of the $x$x-intercepts.
Write all solutions on the same line separated by a comma.
State the equation of the axis of symmetry.
Find the coordinates of the vertex.
Vertex $=$=$\left(\editable{},\editable{}\right)$(,)
Graph the parabola.
Loading Graph...
Question 3
Consider the graph.
Determine the coordinates of the vertex of the parabola.
Vertex $=$=$\left(\editable{},\editable{}\right)$(,)
Given that the graph has equation of the form $y=a\left(x-h\right)^2+k$y=a(x−h)2+k, determine the equation of the parabola.
Finding the equation of a quadratic function
We may also be asked to find the equation of a parabola, given a sketch or relevant pieces of information. Using the vertex and factored forms of quadratic functions can be very helpful. Recall that every quadratic expression can be written in factored form as $a\left(x-\alpha\right)\left(x-\beta\right)$a(x−α)(x−β) for the $x$x-intercepts or $a\left(x-h\right)^2+k$a(x−h)2+k for the vertex, where $a$a is simply the coefficient from the general form $y=ax^2+bx+c$y=ax2+bx+c.
We can use the $x$x-intercepts or the coordinates of the vertex to put the equation in the relevant form (factored or vertex form), and then solve for $a$a by substituting the coordinates of any additional point.
Practice questions
Question 4
Form a monic quadratic equation which has solutions $x=-3$x=−3 and $x=-5$x=−5. Express the equation in expanded form.
Question 5
Consider the quadratic $y=x^2-12x+32$y=x2−12x+32
Find the zeros of the quadratic function by completing the square. Write both solutions on the same line, separated by a comma.
Express the equation in the form $y=a\left(x-h\right)^2+k$y=a(x−h)2+k by completing the square.
Find the coordinates of the vertex of the parabola represented by this quadratic function.
Vertex $=$=$\left(\editable{},\editable{}\right)$(,)
Use the zeros and the vertex found in the previous parts to plot the curve.
Loading Graph...