In section 3.05, we used angles of elevation and depression to compare the vertical positions of two or more objects.
Angles can also be used to compare the position of objects on the ground. For this, we use bearings. In this section we will look at the two different ways to measure and use bearings: as true bearings or as compass bearings.
Both of these kinds of bearing use the standard compass rose, which describes four main directions that are known as cardinal directions. Going clockwise from the top of the compass, they are north (N), east (E), south (S) and west (W).

There are also directions exactly half-way between each of these, such as northeast (NE) and southwest (SW). For all of the other possible directions, we will need to use either true or compass bearings.
True bearings
The first way to use bearings is to measure the position of an object by measuring the angle of rotation from due North. This method is helpful in surveying and air navigation to find the location of an object.
In the image below, we want to measure the true bearing of the plane at point $B$B from the airport at point $A$A.
To measure the true bearing, we place the airport at the center of the compass. We then start from the north line and rotate clockwise until we get to the line $AB$AB. This angle is the true bearing of point $B$B from point $A$A.

So, the true bearing of $B$B from $A$A is $127^\circ$127° or $127^\circ$127°T.
When writing true bearings, we always use $3$3 digits to describe the angle. If the angle measure is less than $100^{\circ}$100∘, then we would write something like $040^{\circ}$040∘ or $040^{\circ}$040∘T. This makes it clear that we are talking about a true bearing measurement.
Compass bearings
The aim of a compass bearing is to identify which quadrant of the compass an object is in and then to describe a specific direction within that quadrant.
The compass bearing from point $A$A to point $B$B is the angle from either the north or south line to the path between point $A$A and point $B$B, measured in either an east or west direction.
- Determine whether point $B$B is closest to North or South.
- Start from North or South, then determine how many degrees you need to rotate towards either the East or the West.
When we write the bearing, we describe which line we measured from and which direction we measured in. If we started from North, then rotated $42^\circ$42° west to get to a position $B$B, we would describe the compass bearing of $B$B as $N$N$42^\circ$42°$W$W.
Let's go back to the image of the plane from the airport. This time we want to measure the position of $B$B from $A$A as a compass bearing.
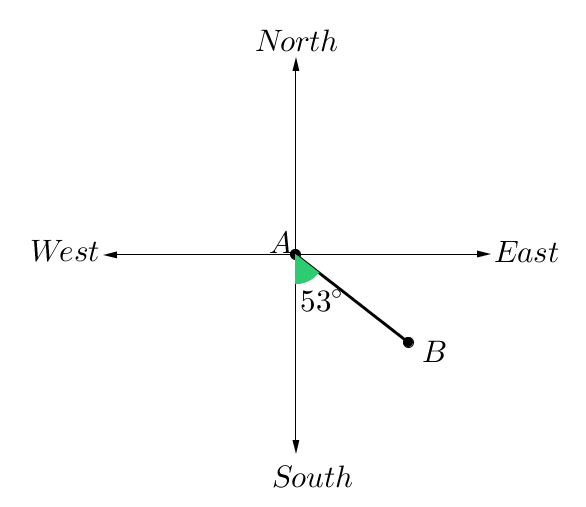
So, a compass bearing always tells us:
- the two cardinal directions the point lies between, and
- the acute angle we need to rotate from either the north or south line to get to the point.
Notice that measuring from $A$A, $B$B is closer to south line than the north line. So we start from South, and then rotate $53^\circ$53° in the easterly direction to get to $B$B.
Describing the position of $B$B, we can say: "Starting at the south line, I then rotate $53^\circ$53° in an east direction."
So, the compass bearing from $A$A to $B$B will be $S$S$53^\circ$53°$E$E.
From where to where?
Remember that the bearing between two objects depends on which point we are measuring to and which point we are measuring from. Keep an eye out for which point is the 'from' point and which is the 'to' point in order to calculate the correct bearing.
Example 1
Find the compass bearing of point $P$P from $O$O.
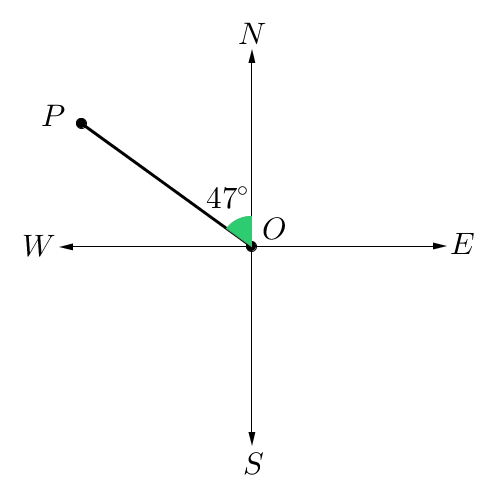
Point $P$P is in the northwest quadrant. So starting at the north line, we can rotate $47^\circ$47° in a west direction to get to the path from $O$O to $P$P.
This means that the compass bearing of $P$P from $O$O is $N$N$47^\circ$47°$W$W.
Example 2
Consider the point $A$A.

Find the true bearing of $A$A from $O$O.
What is the compass bearing of point $A$A from $O$O?
$\editable{}$ $\editable{}$° $\editable{}$
Example 3
What is the true bearing of southwest?
Example 4
In the figure below, Point $B$B is due east of point $A$A.

Find the true bearing of Point $A$A from Point $C$C.
What is the compass bearing of Point $A$A from Point $C$C?
$\editable{}$ $\editable{}$° $\editable{}$