Class XI

Applications of maximisation and minimisation

Lesson

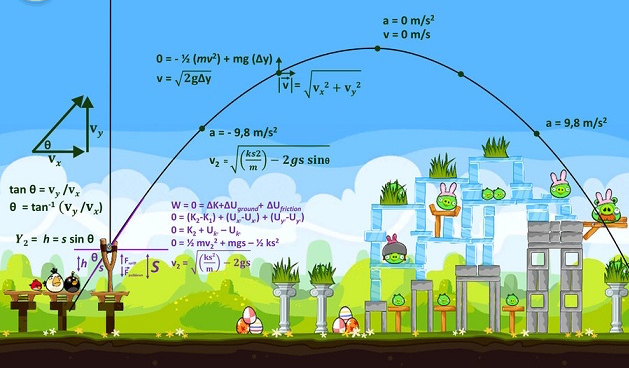
You may have found yourself sitting in maths class asking, "This is great but when am I actually going to use this in the real world?!" Well, although it's not always obvious, we use all different kinds of maths all the time. In this chapter we are going to look at the application of minimum and maximum values of parabolas in the real world. Although engineers and astronauts may use them frequently in their jobs, any person that's played Angry Birds, Super Mario or Donkey Kong has also dabbled in the world of parabolas. But don't worry - our calculations won't be as complex as the ones in the picture above!

For example, in the world of Super Mario we jump in a certain parabolic shape to a certain height. This will allow us to reach coins that are up high. However, if we use a running jump and push off more to the side, we won't jump as high (that is, we've decreased the maximum value) but we will jump further (that is, we've increased the width of the parabola).

Remember!

Parabolas that are concave up have a minimum value and parabolas that are concave down have a maximum value.

Recap

We've looked at how to find the minimum or maximum values. The process goes:

1. Determine whether the parabola is concave up or concave down so we know whether we're finding a minimum or maximum value.

2. Calculate the equation of the axis of symmetry.

3. Substitute the value from Step 2 (which will be the $x$x-coordinate of the turning point) into the original equation to find the value of the dependent variable (which will be the $y$y-coordinate of the turning point).

Let's work through some examples now using this process.

Examples

Question 1

The sum of two whole numbers is $24$24. Let one of the numbers be $x$x.

Let $y$y represent the product of the numbers. Form an expression for $y$y in terms of $x$x.

Enter each line of work as an equation.
Solve for the value of $x$x that will result in the greatest product of the two numbers.

Enter each line of work as an equation.
Find the greatest possible product of the two numbers.

Question 2

A rectangle is to be constructed with $80$80 metres of wire. The rectangle will have an area of $A=40x-x^2$A=40x−x2, where $x$x is the length of one side of the rectangle.

Using the equation, state the area of the rectangle if one side is $12$12 metres long.
The graph below displays all the possible areas that can be obtained using this amount of wire. From the graph, determine the nearest value for the longer side of a rectangle that has an area of $256$256 square metres.

Loading Graph...

A Cartesian plane featuring an horizontal axis labeled "x," ranging from 0 to $40$40, marked at intervals of $4$4. The vertical axis labeled "A," extends from 0 to $400$400, marked at intervals of $100$100 with minor tick marks every $20$20 units. A parabola is graphed on this plane, with its vertex positioned at ($20$20, $400$400) opening downward and passes through the origin and ($40$40, 0). Its coordinates of the vertex and y-intercept are not explicitly labeled or given.

$33$33 m
A
$9$9 m
B
$8$8 m
C
$32$32 m
D
Using the graph, what is the greatest possible area of a rectangle that has a perimeter of $80$80 m?
Using the graph, state the dimensions of the rectangle with the maximum area.

Length $=$=$\editable{}$ m

Width $=$=$\editable{}$ m

Outcomes

11.CG.CS.1

Sections of a cone: Circles, ellipse, parabola, hyperbola, a point, a straight line and pair of intersecting lines as a degenerated case of a conic section. Standard equations and simple properties of parabola, ellipse and hyperbola. Standard equation of a circle.